单选题 (共 6 题 ),每题只有一个选项正确
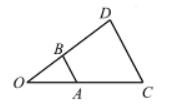
如图, 以点 $O$ 为位似中心, 将 $\triangle O A B$ 放大后得到 $\triangle O C D, O A=3, A C=4$, 则 $\frac{A B}{C D}$ 等于
$\text{A.}$ $\frac{3}{7}$
$\text{B.}$ $\frac{4}{7}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{3}{5}$
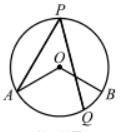
如图, 在 $\odot O$ 中, $\angle A O B=120^{\circ}$, 点 $P 、 Q$ 分别是 $\overparen{A P B}$ 与 $\overparen{A B}$ 上的动点, 则 $\angle A P Q$ 的度数不可能是
$\text{A.}$ $50^{\circ}$
$\text{B.}$ $55^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $65^{\circ}$
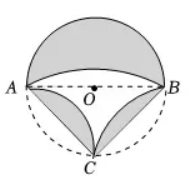
如图, 在 $\odot O$ 中, $A B$ 为直径, 点 $C$ 是圆上一点, 连接 $A C, B C$, 以 $C$ 为圆心, $A C$ 的长为半径作弧, 恰好经过点 $B$, 将 $\odot O$ 分别沿 $A C$, $B C$ 向内翻折若 $A B=4$, 则图中阴影部分的面积是
$\text{A.}$ $4 \pi-2$
$\text{B.}$ $16 \pi-2$
$\text{C.}$ $2 \pi$
$\text{D.}$ $14 \pi$
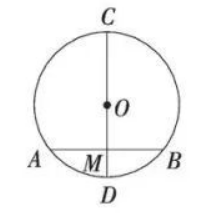
如图, 以 $C D$ 为直径的 $\odot O$ 中, 弦 $A B \perp C D$ 于 $M, A B=16, C M=16$, 则 $M D$ 的长为
$\text{A.}$ 4
$\text{B.}$ 6
$\text{C.}$ 8
$\text{D.}$ 10
已知一个底面半径为 $3 \mathrm{~cm}$ 的圆锥,它的母线长是 $5 \mathrm{~cm}$ ,则这个圆雉的侧面积是 ( ) $\mathrm{cm}^2$
$\text{A.}$ $15 \pi$
$\text{B.}$ $45 \pi$
$\text{C.}$ $30 \pi$
$\text{D.}$ $20 \pi$
如图,已知 $A B$ 是 $\odot O$ 的直径, $C D$ 是 $O O$ 的弦, $A B \perp C D$. 垂足为 $E$. 若 $A B=26 , C D=24 ,$ 则 $\angle O C E$ 的余弦值为
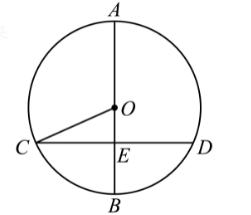
$\text{A.}$ $\frac{7}{13}$
$\text{B.}$ $\frac{12}{13}$
$\text{C.}$ $\frac{7}{12}$
$\text{D.}$ $\frac{13}{12}$