单选题 (共 5 题 ),每题只有一个选项正确
设函数 $f(x)=\lim _{n \rightarrow \infty} \sqrt[n]{1+|x|^{3 n}}$, 则 $f(x)$在 $(-\infty,+\infty)$ 内 ( )
$\text{A.}$ 处处可导.
$\text{B.}$ 恰有一个不可导点.
$\text{C.}$ 恰有两个不可导点.
$\text{D.}$ 至少有三个不可导点.
设函数 $f(x)$ 连续, 且 $f^{\prime}(0)>0$, 则存在 $\delta>0$, 使得
$\text{A.}$ $f(x)$ 在 $(0, \delta)$ 内单调增加.
$\text{B.}$ $f(x)$ 在 $(-\delta, 0)$ 内单调减少.
$\text{C.}$ 对任意的 $x \in(0, \delta)$, 有 $f(x)>f(0)$.
$\text{D.}$ 对任意的 $x \in(-\delta, 0)$, 有 $f(x)>f(0)$.
设函数 $f(x)$ 具有 2 阶导数, $g(x)=f(0)(1-x)+f(1) x$,则在区间 $[0,1]$ 上 ( )
$\text{A.}$ 当 $f^{\prime}(x) \geq 0$ 时, $f(x) \geq g(x)$.
$\text{B.}$ 当 $f^{\prime}(x) \geq 0$ 时, $f(x) \leq g(x)$.
$\text{C.}$ 当 $f^{\prime \prime}(x) \geq 0$ 时, $f(x) \geq g(x)$.
$\text{D.}$ 当 $f^{\prime \prime}(x) \geq 0$ 时, $f(x) \leq g(x)$.
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 内连续, 其导函数的图形如图所示, 则
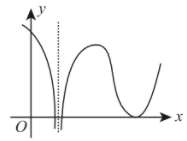
$\text{A.}$ 函数 $f(x)$ 有 2 个极值点, 曲线 $y=f(x)$ 有 2 个拐点.
$\text{B.}$ 函数 $f(x)$ 有 2 个极值点, 曲线 $y=f(x)$ 有 3 个拐点.
$\text{C.}$ 函数 $f(x)$ 有 3 个极值点, 曲线 $y=f(x)$ 有 1 个拐点.
$\text{D.}$ 函数 $f(x)$ 有 3 个极值点,曲线 $y=f(x)$ 有 2 个拐点.
已知函数 $f(x)=\left\{\begin{array}{ll}2(x-1), & x < 1, \\ \ln x, & x \geq 1,\end{array}\right.$ 则 $f(x)$ 的一个原函数是 ( )
$\text{A.}$ $F(x)= \begin{cases}(x-1)^2, & x < 1, \\ x(\ln x-1), & x \geq 1 .\end{cases}$
$\text{B.}$ $F(x)= \begin{cases}(x-1)^2, & x < 1, \\ x(\ln x+1)-1, & x \geq 1 .\end{cases}$
$\text{C.}$ $F(x)= \begin{cases}(x-1)^2, & x < 1, \\ x(\ln x+1)+1, & x \geq 1 .\end{cases}$
$\text{D.}$ $F(x)= \begin{cases}(x-1)^2, & x < 1, \\ x(\ln x-1)+1, & x \geq 1 .\end{cases}$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
曲线 $y=\left(1+\frac{1}{x}\right)^{x-1}$ 有水平渐近线 ________ 和铅直渐近线 ________