单选题 (共 6 题 ),每题只有一个选项正确
已知二元函数 $F(x, y)=f(x, y) \varphi(x, y)$ ,其中 $\varphi(x, y)$ 在点 $(0,0)$ 处连续,且 $f(0,0)=0$ , $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} f_x^{\prime}(x, y)=\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} f_y^{\prime}(x, y)=0$ ,则 $F(x, y)$ 在点 $(0,0)$ 处 $(\quad)$ .
$\text{A.}$ 不连续
$\text{B.}$ 连续,但偏导数不存在
$\text{C.}$ 连续,偏导数存在但不可微
$\text{D.}$ 可微
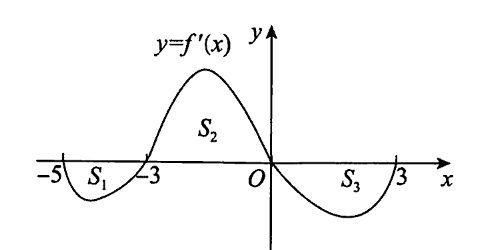
已知 $f(0)=-1$ ,导数 $f^{\prime}(x)$ 在 $[-5,3]$ 上连续,曲线 $y=f^{\prime}(x)$ 与直线 $x=-5, x=3$ 及 $x$轴围成的图像如图所示,相应的面积分别为 $S_1=2, S_2=4, S_3=3$ ,记 $f(x)$ 在 $[-5,3]$ 上的最大值为 $M$ ,最小值为 $m$ ,则 $M-m=(\quad)$ .
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
下列说法正确的个数是( )
(1)若 $\lim _{x \rightarrow 0} f(x)=0$ ,则 $\lim _{x \rightarrow 0} f(x) \sin \frac{1}{x}=0$ ;
(2)若 $\lim _{x \rightarrow 0} f(x) \sin \frac{1}{x}=0$ ,则 $\lim _{x \rightarrow 0} f(x)=0$ ;
(3)若 $f(x)$ 在 $x=0$ 的去心邻域内无界,则 $f(x) \sin \frac{1}{x}$ 在 $x=0$ 的去心邻域内无界;
(4)若 $f(x) \sin \frac{1}{x}$ 在 $x=0$ 的去心邻域内无界,则 $f(x)$ 在 $x=0$ 的去心邻域内无界。
$\text{A.}$ 1.
$\text{B.}$ 2 .
$\text{C.}$ 3.
$\text{D.}$ 4 .
设 $y=y(x)$ 为微分方程 $2 x y d x+\left(x^2-1\right) d y=0$ 满足初始条件 $y(0)=1$ 的特解,则 $\int_0^{\frac{1}{2}} y(x) d x=(\quad)$.
$\text{A.}$ $-\ln 3$
$\text{B.}$ $\ln 3$
$\text{C.}$ $-\frac{1}{2} \ln 3$
$\text{D.}$ $\frac{1}{2} \ln 3$
设 $D$ 是由曲线 $2 x y=1$ 与直线 $x+y=\frac{3}{2}$ 所围成的封闭区域,已知函数 $f(x, y)$ 在区域 $D$ 上连续,则 $\iint_D f(x, y) \mathrm{d} x \mathrm{~d} y=$
$\text{A.}$ $2 \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \mathrm{~d} \theta \int_{\frac{1}{\sqrt{\sin 2 \theta}}}^{\frac{3}{2(\sin \theta+\cos \theta)}} f(r \cos \theta, r \sin \theta) r \mathrm{~d} r$ .
$\text{B.}$ $2 \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \mathrm{~d} \theta \int_{\frac{1}{\sqrt{2 \sin 2 \theta}}}^{\frac{3}{2(\sin \theta+\cos \theta)}} f(r \cos \theta, r \sin \theta) r \mathrm{~d} r$ .
$\text{C.}$ $2 \int_{\frac{\pi}{4}}^{\arctan 2} \mathrm{~d} \theta \int_{\frac{1}{\sqrt{\sin 2 \theta}}}^{\frac{3}{2(\sin \theta+\cos \theta)}} f(r \cos \theta, r \sin \theta) r \mathrm{~d} r$ .
$\text{D.}$ $2 \int_{\frac{\pi}{4}}^{\arctan 2} \mathrm{~d} \theta \int_{\frac{1}{\sqrt{2 \sin 2 \theta}}}^{\frac{3}{2(\sin \theta+\cos \theta)}} f(r \cos \theta, r \sin \theta) r \mathrm{~d} r$ .
曲线 $y=\frac{3 x^3}{2-x^2}+\operatorname{arccot}(x+2)$ 的渐近线条数为
$\text{A.}$ 4 .
$\text{B.}$ 3 .
$\text{C.}$ 2.
$\text{D.}$ 1 .