填空题 (共 9 题 ),请把答案直接填写在答题纸上
设 $u$ 轴与三坐标轴正向构成相等的锐角,求空间向量 $a =(4,-3,2)$ 在 $u$ 轴上的投影
一平面 $\pi$ 过球面 $x^2+y^2+z^2=4 x-2 y-2 z$ 的球心,并垂直于直线 $l:\left\{\begin{array}{l}x=0, \\ y+z=0\end{array}\right.$ ,求该平面与该球面的交线在 $x O y$ 坐标面上的投影.
设曲面 $\Sigma$ 是由 $y O z$ 平面上的双曲线 $z^2-4 y^2=2$ 绕 $z$ 轴旋转而成,曲面上一点 $M$ 处的切平面 $\Pi$与平面 $x+y+z=0$ 平行,写出曲面 $\Sigma$ 和切平面 $\Pi$ 的方程.
设函数 $z=x f\left(x y+\frac{y}{x}\right)$ ,其中 $f$ 二阶可微,求 $\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}$ 和 $\frac{\partial^2 z}{\partial x \partial y}$ .
设方程 $x^2+y^2+z^2-4 z=0$ 确定函数 $z=z(x, y)$ ,求 $\frac{\partial z}{\partial x}, \frac{\partial^2 z}{\partial x^2}$ 和 $\frac{\partial^2 z}{\partial x \partial y}$ .
已知 $\frac{\partial f}{\partial x}=2 x y-y^4+3, \frac{\partial f}{\partial y}=x^2-4 x y^3$ ,求函数 $f(x, y)$ .
计算累次积分 $\int_0^1 d y \int_{\sqrt{y}}^1 \sqrt{1+x^3} d x$ .
设 $D: x^2+y^2 \leq 9$ ,计算二重积分 $\iint_D\left|x^2+y^2-4\right| d x d y$ .
设 $L$ 为曲线 $\frac{x^2}{4}+\frac{y^2}{3}=1$ ,其周长为 $a$ ,计算曲线积分 $\int_L\left(3 x^2+4 y^2+2 x y\right) d s$ .
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $\Sigma$ 为介于 $z=0$ 和 $z=h$ 之间的圆柱面 $x^2+y^2=R^2$ ,计算 $\iint_{\Sigma} \frac{ d S}{x^2+y^2+z^2}$ .
设曲面 $\Sigma: x^2+y^2=z(0 \leq z \leq h)$ 的法方向与 $z$ 轴正向的夹角为钝角,求流体速度场 $v =(x+y+z) k$ 在单位时间内流过该曲面 $\Sigma$ 的流量.
设一个密度均匀的半球体占有空间区域 $\Omega: x^2+y^2+z^2 \leq R^2, z \geq 0$ ,试求该半球体质心的坐标.
设有一座山的万程为 $z=75-x^2-y^2+x y, M\left(x_0, y_0\right)$ 是山脚 $z=0$(即等高线 $x^2+y^2-x y=75$上)的点.(1)问 $z$ 在点 $M\left(x_0, y_0\right)$ 处沿什么方向的增长率最大,若记此增长量的最大值为 $\varphi\left(x_0, y_0\right)$ ,试求出 $\varphi\left(x_0, y_0\right) ;(2)$ 现欲利用此山开展攀岩活动,为此需要在山脚处找一坡度最陡的位置作为攀岩的起点,即在上述等高线上找一点 $M$ ,使得上述增长率最大,试确定该起点的位置.
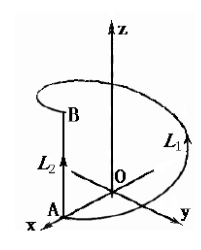
如图,设力场 $F =y i -x j +(x+y+z) k$ ,(1)求一质点由 $A$ 沿圆柱螺线 $L_1$ 到 $B$ 时,力 F 所做的功,其中螺线 $L_1$ 的方程为 :$x=a \cos t, y=a \sin t, z=\frac{c}{2 \pi} t$ ;(2)求该质点由 $A$沿直线 $L_2$ 到 $B$ 时,力 F 所做的功;(3)简述上面所求结果不相等的原因;就一般情况而言, F 是否可以满足一定的条件使其由 $A$ 到 $B$ 所做的功相等?这个条件是什么?
若 $L$ 为平面上任一不经过原点的逆时针圆周,试计算积分 $\int_L \frac{x d y-y d x}{x^2+4 y^2}$ 的值.