单选题 (共 6 题 ),每题只有一个选项正确
下列运算中,正确的是
$\text{A.}$ $m^3+m^3=2 m^3$
$\text{B.}$ $m^3+m^3=m^6$
$\text{C.}$ $m^3 \cdot m^3=m^9$
$\text{D.}$ $\left(m^3\right)^3=m^6$
下列代数式中,能表示"$x$ 与 $y$ 的差的平方"的是
$\text{A.}$ $x^2-y^2$
$\text{B.}$ $(x-y)^2$
$\text{C.}$ $x^2-y$
$\text{D.}$ $x-y^2$
下列函数中,是正比例函数的是
$\text{A.}$ $y=3 x+1$
$\text{B.}$ $y=3 x^2$
$\text{C.}$ $y=\frac{3}{x}$
$\text{D.}$ $y=\frac{x}{3}$
如图是某校体育组 60 人的某科成绩,下列说法中正确的是
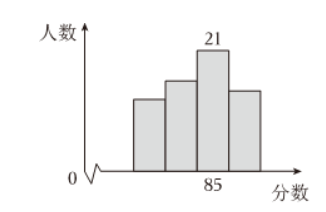
$\text{A.}$ 中位数是 21
$\text{B.}$ 中位数是 85
$\text{C.}$ 众数是 21
$\text{D.}$ 众数是 85
在正方形 $A B C D$ 中,$|\overrightarrow{A B}+\overrightarrow{B C}|$ :$|\overrightarrow{C D}|$ 的值是()
$\text{A.}$ $\frac{\sqrt{2}}{2}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\sqrt{2}$
$\text{D.}$ 2
在锐角三角形 $A B C$ 中,$A B=A C, B C=8$ ,它的外接圆 $O$ 的半径长为 5 ,若点 $D$ 是边 $B C$ 的中点,以点 $D$ 为圆心的圆和 $\odot O$ 相交,那么 $\odot D$ 的半径长可以是( )
$\text{A.}$ 2
$\text{B.}$ 5
$\text{C.}$ 8
$\text{D.}$ 10
填空题 (共 12 题 ),请把答案直接填写在答题纸上
不等式组 $\left\{\begin{array}{l}\frac{x}{2}-1>0 \\ 2 x+3 \geq x\end{array}\right.$ 的解集是
一元二次方程 $2 x^2+x+m=0$ 没有实数根,那么 $m$ 的取值范围是
抛物线 $y=3 x^2$ 向下平移两个单位所得的抛物线解析式为
已知一个反比例函数,在每个象限内,函数值 $y$ 随 $x$ 的增大而减小,那么这个反比例函数的解析式可以是
小明手中有 $1 、 2 、 3 、 4$ 四张牌,小军手中有 $2 、 4 、 6 、 8$ 四张牌,若小明从小军手中抽一张牌,抽到任何牌的概率相等,那么抽到的牌和自己原有的牌的数字相等的概率为
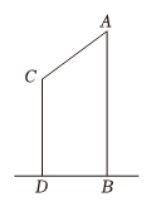
如图,某公司安装了一个人脸打卡器,$A B$ 是高 2.7 m 的门框,某人 $C D$ 高 1.8 m ,只有当 $\angle C A B=53^{\circ}$ 时,他才能开门,那么 $B D$ 长为 $\qquad$ .(参考数据: $\sin 53^{\circ} \approx 0.8, \cos 53^{\circ} \approx 0.6, \tan 53^{\circ} \approx 1.33$ ,保留1位小数)
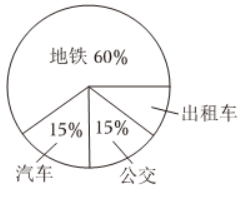
某高铁站出站后有出租车、地铁、汽车、公交等出行方式,高铁站为调查各个出行方式的人流,先对 2000 人展开调查,结果如图所示,那么某日高铁站出站客流约为 1.8 万人,其中有约
$\qquad$人选择出租车.
已知我国通过科技,研究出了一种超皮秒工具,进行一次擦除仅仅需要 400 皮秒,已知 1 皮秒等于 $1 \times 10^{-12}$ 秒,那么这个工具 1 秒可以擦除 $\qquad$次(用科学记数法表示)。
已知矩形 $A B C D$ 中,点 $E$ 在边 $C D$ 上,$F$ 是点 $E$ 关于直线 $A D$ 的对称点,联结 $E F 、 A F 、 B E$ ,若四边形 $A B E F$ 是菱形,那么 $\frac{A B}{A D}$ 的值为
已知平面内有一个角,一个圆与这个角的两边都有两个交点,若此圆在角的边上截得的两条弦恰好是某正五边形的一边,那么这个角的度数为 $\qquad$度.
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算:$\frac{4}{\sqrt{5}+1}-20^{\frac{1}{2}}+|2-\sqrt{5}|+\left(\frac{1}{2}\right)^{-3}$ .
解方程:$\frac{x-3}{x-2}-\frac{2}{x^2-3 x+2}=\frac{2}{x-1}$
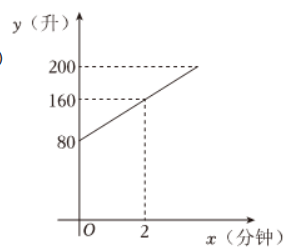
某品牌储水机的容量是 200 升,当加水加满时,储水机会自动停止加水,已知加冷水量 $y$(升)和时间 $x$(分钟)的图象如图所示,加水过程中,水的温度 $t$(摄氏度)和 $x$(分钟)的关系:$t=\frac{20 x+100}{x+2}$ .
(1)求 $y$ 与 $x$ 的函数关系式,并写出定义域;
(2)求储水机中的水加满时,储水机内水的温度。
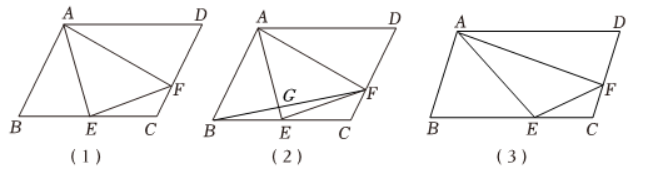
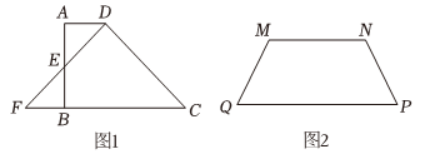
某小组对分割梯形组成等腰三角形展开研究.
(1)如图1,梯形 $A B C D$ 中,$A D \| B C, A B \perp B C$ ,点 $E$ 是 $A B$ 中点,$D$ 是梯形的顶点,将 $\triangle A D E$ 绕 $E$ 旋转 $180^{\circ}$ 得到 $\triangle B F E$ ,若 $A D=a$ ,且此时 $D F=D C$ ,求 $B C$ 的长(用含 $a$ 的代数式尝试表示);
(2)如图2,梯形 $M N P Q, M N \| P Q, M Q=N P$ ,请设计一种方法,用一条直线或两条直线分割梯形为若干部分,再进行一系列的图形运动,拼成一个等腰三角形,在图2中画出图形,要求:(1)所得的部分不重叠,不间隙地拼;(2)在答题纸横线上并写出等腰三角形的腰是哪条线段;(3)在答题纸横线上写出这一或两条直线的顶点.(模仿 1 中的表述:点 $E$ 是 $A B$ 中点,$D$ 是梯形的顶点)
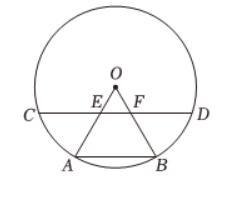
如图,在 $\odot O$ 中,$A B$ 和 $C D$ 是弦,半径 $O A 、 O B$ 分别交 $C D$ 于点 $E 、 F$ ,且 $C E=D F$ .
(1)求证:$A B \| C D$ ;
(2)若 $A B=B D$ ,求证:$A B^2=B F \cdot O B$ .
在平面直角坐标系 $x O y$ 中,抛物线 $y=x^2+b x+c$ 经过点 $A(1,1)$ 和 $B(3,1)$ ,顶点为点 $P$ ,抛物线于 $y$ 轴交于点 $C$ 。
(1)求 $b$ 和 $c$ 的值.
(2)另一条抛物线 $y=a x^2+m x+n(a \neq 1)$ 也经过点 $A(1,1)$ 和 $B(3,1)$ ,顶点为点 $Q$ ,与 $y$ 轴交于点 $D$ .
① 求 $\frac{C D}{P Q}$ 的值;
② 当四边形 $C D P Q$ 是直角梯形,求其最小内角的正弦值.
如图1,平行四边形 $A B C D$ 中,点 $E 、 F$ 分别是边 $B C 、 C D$ 上的点.
(1)若 $E$ 是 $B C$ 中点;
① 如图1,若 $A E=E F$ ,求证:$\angle B A E=\angle E F C$ ;
② 如图2,若 $C F=D F$ ,联结 $B F$ 交 $A E$ 于 $G$ ,求 $S_{\triangle B E G}: S_{\triangle A E F}$ 的值;
(2)如图3,若 $A B=3, A D=5, C F=1, \angle A E B=\angle A F E=\angle E F C$ ,求 $A F$ 的长.