单选题 (共 10 题 ),每题只有一个选项正确
集合 $M=\{x \mid 2 x-1>5\}, N=\{1,2,3\}$ ,则 $M \cap N=()$
$\text{A.}$ $\{1,2,3\}$
$\text{B.}$ $\{2,3\}$
$\text{C.}$ $\{3\}$
$\text{D.}$ $\varnothing$
已知复数 $z$ 满足 $i \cdot z+2=2 i$ ,则 $|z|=$( )
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ 4
$\text{D.}$ 8
双曲线 $x^2-4 y^2=4$ 的离心率为( )
$\text{A.}$ $\frac{\sqrt{3}}{2}$
$\text{B.}$ $\frac{\sqrt{5}}{2}$
$\text{C.}$ $\frac{5}{4}$
$\text{D.}$ $\sqrt{5}$
为得到函数 $y=9^x$ 的图象,只需把函数 $y=3^x$ 的图象上的所有点( )
$\text{A.}$ 横坐标变成原来的 $\frac{1}{2}$ 倍,纵坐标不变
$\text{B.}$ 横坐标变成原来的 2 倍,纵坐标不变
$\text{C.}$ 纵坐标变成原来的 $\frac{1}{3}$ 倍,横坐标不变
$\text{D.}$ 纵坐标变成原来的 3 倍,横坐标不变
已知 $\left\{a_n\right\}$ 是公差不为 0 的等差数列,$a_1=-2$ ,若 $a_3, a_4, a_6$ 成等比数列,则 $a_{10}=()$
$\text{A.}$ -20
$\text{B.}$ -18
$\text{C.}$ 16
$\text{D.}$ 18
已知 $a>0, b>0$ ,则( )
$\text{A.}$ $a^2+b^2>2 a b$
$\text{B.}$ $\frac{1}{a}+\frac{1}{b} \geq \frac{1}{a b}$
$\text{C.}$ $a+b>\sqrt{a b}$
$\text{D.}$ $\frac{1}{a}+\frac{1}{b} \leq \frac{2}{\sqrt{a b}}$
已知函数 $f(x)$ 的定义域为 $D$ ,则"函数 $f(x)$ 的值域为 R "是"对任意 $M \in R$ ,存在 $x_0 \in D$ ,使得 $\left|f\left(x_0\right)\right|>M$"的( )
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充分必要条件
$\text{D.}$ 既不充分也不必要条件
设函数 $f(x)=\sin (\omega x)+\cos (\omega x)(\omega>0)$ ,若 $f(x+\pi)=f(x)$ 恒成立,且 $f(x)$ 在 $\left[0, \frac{\pi}{4}\right]$ 上存在零点,则 $\omega$ 的最小值为
$\text{A.}$ 8
$\text{B.}$ 6
$\text{C.}$ 4
$\text{D.}$ 3
在一定条件下,某人工智能大语言模型训练 $N$ 个单位的数据量所需要时间 $T=k \log _2 N$(单位:小时),其中 $k$ 为常数.在此条件下,已知训练数据量 $N$ 从 $10^6$ 个单位增加到 $1.024 \times 10^9$ 个单位时,训练时间增加 20 小时;当训练数据量 $N$ 从 $1.024 \times 10^9$ 个单位增加到 $4.096 \times 10^9$ 个单位时,训练时间增加(单位:小时)
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ 20
$\text{D.}$ 40
已知平面直角坐标系 $x O y$ 中,$|\overrightarrow{O A}|=|\overrightarrow{O B}|=\sqrt{2},|\overrightarrow{A B}|=2$ ,设 $C(3,4)$ ,则 $|2 C A+\overrightarrow{A B}|$ 的取值范围是( )
$\text{A.}$ $[6,14]$
$\text{B.}$ $[6,12]$
$\text{C.}$ $[8,14]$
$\text{D.}$ $[8,12]$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
抛物线 $y^2=2 p x(p>0)$ 的顶点到焦点的距离为 3 ,则 $p=$
已知 $(1-2 x)^4=a_0-2 a_1 x+4 a_2 x^2-8 a_3 x^3+16 a_4 x^4$ ,则 $a_0=$ $\qquad$ ;
$a_1+a_2+a_3+a_4=$
已知 $\alpha, \beta \in[0,2 \pi]$ ,且 $\sin (\alpha+\beta)=\sin (\alpha-\beta), \cos (\alpha+\beta) \neq \cos (\alpha-\beta)$ ,写出满足条件的一组 $\alpha=$ $\qquad$ ,$\beta=$
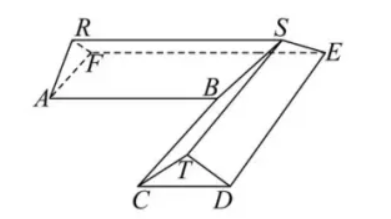
某科技兴趣小组通过 3D 打印机的一个零件可以抽象为如图所示的多面体,其中 $A B C D E F$是一个平行多边形,平面 $A R F \perp$ 平面 $A B C$ ,平面 $T C D \perp$ 平面 $A B C$ , $A B \perp B C, A B / / R S / / E F / / C D, A F / / S T / / B C / / E D$ ,若 $A B=B C=8, A F=C D=4, A R=R F=T C=T D=\frac{5}{2}$ ,则该多面体的体积为 $\qquad$ .
关于定义域为 $R$ 的函数 $f(x)$ ,以下说法正确的有 $\qquad$。
(1)存在在 $R$ 上单调递增的函数 $f(x)$ ,使得 $f(x)+f(2 x)=-x$ 恒成立;
(2)存在在 $R$ 上单调递减的函数 $f(x)$ ,使得 $f(x)+f(2 x)=-x$ 恒成立;
(3)使得 $f(x)+f(-x)=\cos x$ 恒成立的函数 $f(x)$ 存在且有无穷多个;
(4)使得 $f(x)-f(-x)=\cos x$ 恒成立的函数 $f(x)$ 存在且有无穷多个.
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在三角形 $A B C$ 中, $\cos A=-\frac{1}{3}, a \sin C=4 \sqrt{2}$ .
(1)求 $c$ ;
(2)在以下三个条件中选择一个作为已知,使得 $ A B C$ 存在,求 $B C$ 的高.
① $a=6$ ;
② $b \sin C=\frac{10 \sqrt{2}}{3}$ ;
③ $ A B C$ 面积为 $10 \sqrt{2}$ .
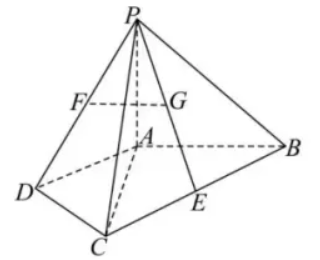
四棱锥 $P-A B C D$ 中,$\triangle A C D$ 与 $V A B C$ 为等腰直角三角形,$\angle A D C=90^{\circ}, \angle B A C=90^{\circ}$ , $E$ 为 $B C$ 的中点.
(1)$F$ 为 $P D$ 的中点,$G$ 为 $P E$ 的中点,证明:$F G / /$ 平面 $P A B$ ;
(2)若 $P A \perp$ 平面 $A B C D, P A=A C$ ,求 $A B$ 与平面 $P C D$ 所成角的正弦值.
有一道选择题考查了一个知识点,甲、乙两校各随机抽取 100 人,甲校有 80 人答对,乙校有 75 人答对,用频率估计概率.
(1)从甲校随机抽取 1 人,求这个人做对该题目的概率.
(2)从甲、乙两校各随机抽取 1 人,设 $X$ 为做对的人数,求恰有 1 人做对的概率以及 $X$ 的数学期望.
(3)若甲校同学掌握这个知识点,则有 $100 \%$ 的概率做对该题目,乙校同学掌握这个知识点,则有 $85 \%$ 的概率做对该题目,未掌握该知识点的同学都是从四个选项里面随机选择一个,设甲校学生掌握该知识点的概率为 $p_1$ ,乙校学生掌握该知识点的概率为 $p_2$ ,试比较 $p_1$ 与 $p_2$的大小(结论不要求证明)
19.已知 $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ,椭圆上的点到两焦点距离之和为 4 ,
(1)求椭圆方程;
(2)设 $O$ 为原点,$M\left(x_0, y_0\right)\left(x_0 \neq 0\right)$ 为椭圆上一点,直线 $x_0 x+2 y_0 y-4=0$ 与直线 $y=2, y=-2$交于 $A, B$ .$\triangle O A M$ 与 $\triangle O B M$ 的面积为 $S_1, S_2$ ,比较 $\frac{S_1}{S_2}$ 与 $\frac{|O A|}{|O B|}$ 的大小.
函数 $f(x)$ 的定义域为 $(-1,+\infty), f(0)=0, f^{\prime}(x)=\frac{\ln (1+x)}{1+x}, l_1$ 为 $A(a, f(a))(a \neq 0)$ 处的切线.
(1)$f^{\prime}(x)$ 的最大值;
(2)证明:当 $-1 < a < 0$ 时,除点 $A$ 外,曲线 $y=f(x)$ 均在 $l_1$ 上方;
(3)若 $a>0$ 时,直线 $l_2$ 过 $A$ 且与 $l_1$ 垂直,$l_1, l_2$ 分别于 $x$ 轴的交点为 $x_1$ 与 $x_2$ ,求 $\frac{2 a-x_1-x_2}{x_2-x_1}$ 的取值范围.
$A=\{1,2,3,4,5,6,7,8\}, M=\left\{\left(x_i, y_i\right) \mid x_i \in A, y_i \in A\right\}$ ,从 $M$ 中选出 $n$ 个有序数对构成一列: $\left(x_1, y_1\right), \ldots,\left(x_n, y_n\right)$ .相邻两项 $\left(x_i, y_i\right),\left(x_{i+1}, y_{i+1}\right)$ 满足:$\left\{\begin{array}{l}\left|x_{i+1}-x_i\right|=3 \\ \left|y_{i-1}-y_i\right|=4\end{array}\right.$ 或 $\left\lvert\, \begin{array}{l}\left|x_{i+1}-x_i\right|=4 \\ \left|y_{i+1}-y_i\right|=3\end{array}\right.$, 称为 $k$ 列.
(1)若 $k$ 列的第一项为 $(3,3)$ ,求第二项.
(2)若 $\tau$ 为 $k$ 列,且满足 $i$ 为奇数时,$x_i \in\{1,2,7,8\}: i$ 为偶数时,$x_i \in\{3,4,5,6\}$ ;判断:$(3,2)$与 $(4,4)$ 能否同时在 $\tau$ 中,并说明;
(3)证明:$M$ 中所有元素都不构成 $k$ 列