单选题 (共 8 题 ),每题只有一个选项正确
已知向量 $\vec{a}=(1,3), \vec{b}=(3, x)$, 若 $\vec{a} \perp \vec{b}$, 则 $x$ 等于
$\text{A.}$ 9
$\text{B.}$ 3
$\text{C.}$ -1
$\text{D.}$ -3
已知集合 $A=\{x \mid-1 < x < 3\}, B=\{0, a\}$, 若 $A \cap B$ 中有且仅有一个元素, 则实数 $a$ 的取值范围为
$\text{A.}$ $(-1,3)$
$\text{B.}$ $(-\infty,-1] \cup[3,+\infty)$
$\text{C.}$ $(-3,1)$
$\text{D.}$ $(-\infty,-3] \cup[1,+\infty)$
已知复数 $z_1=2-\mathrm{i}, z_2=a+\mathrm{i}(a \in \mathbf{R})$, 若复数 $z_1 \cdot z_2$ 为纯虚数, 则实数 $a$ 的值为
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ -2
$\text{D.}$ 2
已知 $\cos \alpha \cos \beta=\frac{2}{5}, \cos (\alpha-\beta)=\frac{3}{5}$, 则 $\cos (\alpha+\beta)=$
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{4}{5}$
$\text{D.}$ $\frac{2}{3}$
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{16}=1(a>0)$, 若双曲线的一条渐近线方程为 $4 x+3 y=0$, 则双曲线 $C$ 的离心率为
$\text{A.}$ $\frac{5}{4}$
$\text{B.}$ $\frac{5}{3}$
$\text{C.}$ $\frac{4}{3}$
$\text{D.}$ $\frac{\sqrt{97}}{9}$
在 $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c$, 若 $C=\frac{\pi}{3}, b+b \cos A=a \cos B$, 则 $B$ 的大小为
$\text{A.}$ $\frac{\pi}{6}$
$\text{B.}$ $\frac{\pi}{3}$
$\text{C.}$ $\frac{\pi}{9}$
$\text{D.}$ $\frac{2 \pi}{9}$
已知定义在 R 上的函数 $f(x)$ 满足 $2 f(x)=f(-x)+3 \mathrm{e}^x$, 则曲线 $y=f(x)$ 在点 $(0, f(0))$ 处的切线方程为
$\text{A.}$ $y=3 x+3$
$\text{B.}$ $y=3 x-3$
$\text{C.}$ $y=x+3$
$\text{D.}$ $y=x-3$
如图, 已知正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 $\sqrt{6}$, 圆锥 $A_1 O$ 在正方体 $A B C D-A_1 B_1 C_1 D_1$ 内, 且 $A_1 C$ 垂直圆锥 $A_1 O$ 的底面,当该圆锥底面积最大时, 圆锥体积为
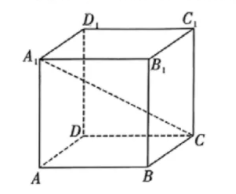
$\text{A.}$ $\frac{3 \sqrt{2}}{2} \pi$
$\text{B.}$ $2 \sqrt{2} \pi$
$\text{C.}$ $\frac{9 \sqrt{2}}{8} \pi$
$\text{D.}$ $\frac{8 \sqrt{2}}{3} \pi$
多选题 (共 3 题 ),每题有多个选项正确
已知数据 $x_1, x_2, x_3, \cdots, x_{10}$, 满足: $x_i-x_{i-1}=2(2 \leqslant \mathrm{i} \leqslant 10)$, 若去掉 $x_1, x_{10}$ 后组成一组新数据, 则新数据与原数据相比,下列说法正确的是
$\text{A.}$ 中位数不变
$\text{B.}$ 若 $x_1=1$, 则数据 $x_1, x_2, x_3, \cdots, x_{10}$ 的第 75 百分位数为 13
$\text{C.}$ 平均数不变
$\text{D.}$ 方差变小
已知定义在区间 $[0, \pi]$ 上的函数 $f(x)=a x+\cos x$, 其中 $a \in \mathrm{R}$, 若函数 $f(x)$ 恰有两个极值点, 设其极大值、极小值分别记为 $m_1, m_2$. 则下列结论正确的是
$\text{A.}$ 函数 $f^{\prime}(x)$ 的图象关于直线 $x=\frac{\pi}{2}$ 对称
$\text{B.}$ 实数 $a$ 的取值范围为 $(0,1)$
$\text{C.}$ $m_1+m_2=a \pi$
$\text{D.}$ $m_1+m_2=a+a \pi$
已知 $F_1, F_2$ 是椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的两个焦点,点 $P$ 在椭圆 $C$ 上, 若 $P F_1 \perp P F_2, \triangle F_1 P F_2$ 的面积等于 4 . 则下列结论正确的是
$\text{A.}$ 若点 $P$ 是椭圆的短轴顶点, 则楠圆 $C$ 的标准方程为 $\frac{x^2}{8}+\frac{y^2}{4}=1$
$\text{B.}$ 若 $P$ 是动点, 则 $b$ 的值恒为 2
$\text{C.}$ 若 $P$ 是动点, 则椭圆的离心率的取值范围是 $\left[\frac{1}{2}, 1\right)$
$\text{D.}$ 若 $P$ 是动点, 则 $\left|P F_1\right|+\left|P F_2\right|$ 的取值范围是 $[4 \sqrt{2},+\infty)$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
将函数 $f(x)=\sin \left(2 x-\frac{\pi}{3}\right)$ 的图象沿 $x$ 轴向左平移 $\frac{\pi}{6}$ 个单位长度后得到函数 $g(x)$ 的图象, 则 $g\left(\frac{\pi}{4}\right)$ 的值为
已知奇函数 $y=f(x)$ 在其定义域 $(-1,1)$ 上是减函数, 且 $f(1-a)+f\left(1-a^2\right) < 0$, 则 $a$ 的取值范围为
某超市为了保证顾客能购买到新鲜的牛奶又不用过多存货, 统计了 30 天销售水牛奶的情况, 获得如下数据
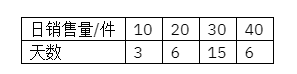
该超市存货管理水平的高低会直接影响超市的经营情况. 该超市对鲜牛奶实行如下存货管理制度: 当天营业结束后检查存货, 若存货少于 30 件, 则通知配送中心立即补货至 40 件, 否则不补货. 假设某天开始营业时货架上有 40 件水牛奶, 则第二天营业结束后货架上有 20 件存货的概率为 $\qquad$ .(以样本估计总体, 将频率视为概率)
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
近年来, 我国新能源汽车进入快车道, 自 2015 年以来, 产销量已经连续八年增长, 位居全球前列. 近期国务院出台了新能源汽车系列政策, 促进了新能源汽车产业的发展. 某市一家知名品牌的新能源汽车企业近
5 个月的产值数据统计如下表:
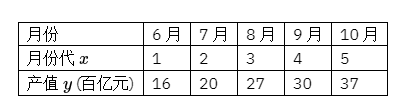
(1) 求出 $y$ 关于 $x$ 的经验回归方程, 并预测明年 3 月份该企业的产值;
(2) 该企业依据市场调研, 为满足消费者的购买需求, 设计并生产了 $A, B, C$ 三种类型新能源汽车, 这三种类型的销量比依次为 $30 \%, 50 \%, 20 \%$, 销售价格依次为 15 万, 25 万, 40 万. 若该新能源汽车的某 $4 S$ 店每天销售 2 台,设销售额为随机变量 $X$, 求 $X$ 的分布列和数学期望.
参考公式: $\hat{b}=\frac{\sum_{i=1}^n x_i y_i-n \bar{x} \bar{y}}{\sum_{i=1}^n x_i^2-n \bar{x}^2}, \hat{a}=\bar{y}-\hat{b} \bar{x}$;参考数据: $\sum_{i=1}^5 x_i y_i=442, \sum_{i=1}^5 x_i^2=55, \bar{y}=26$.
已知抛物线 $C: y^2=2 p x(p>0)$ 的焦点为 $F$, 点 $D\left(x_0, 2\right)$ 在抛物线 $C$ 上, 且 $|D F|=2$.
(1) 求抛物线 $C$ 的标准方程;
(2) 拋物线的准线与 $x$ 轴交于点 $K$, 过 $K$ 的直线 $l$ 交拖物线 $C$ 于 $M, N$ 两点, 且 $\overrightarrow{K M}=\lambda \overrightarrow{K N}(\lambda \in(1,2])$, 点 $G$ 为线段 $M N$ 的垂直平分线与 $x$ 轴的交点,求点 $G$ 的横坐标 $x_G$ 的取值范围.
如图, 在直三棱柱 $A B C-A_1 B_1 C_1$ 中, $D$ 是侧棱 $C C_1$ 的中点, $\angle A C B=120^{\circ}, A A_1=\sqrt{3} A C=\sqrt{3} B C$.
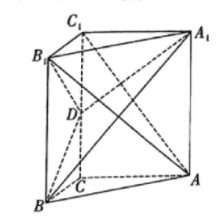
(1) 证明: 平面 $A B_1 C_1 \perp$ 平面 $A_1 B D$;
(2) 求锐二面角 $B-A_1 D-B_1$ 的余弦值.
已知函数 $f(x)=\frac{1}{2} x^2-\ln x, g(x)=\mathrm{e}^{x-1}-\frac{1}{2} x^2-a x(a>0)$.
(1) 求 $f(x)$ 的单调区间;
(2) 设函数 $F(x)=f(x)+g(x)$. 证明:
(i) 函数 $F(x)$ 有唯一极值点;
(ii) 若函数 $F(x)$ 有唯一零点 $x_0$, 则 $1 < x_0 < 2$.
给定整数 $n(n \geqslant 2)$, 数列 $A_{2 n+1}: x_1, x_2, x_3, \cdots, x_{2 n+1}$, 且 $x_k(k=1,2,3, \cdots, 2 n+1)$ 为整数. 在 $A_{2 n+1}$ 中去掉一项 $x_k(k=1,2,3, \cdots, 2 n+1)$, 并将剩下的数分成项数相同的两组, 其中一组数的和与另外一组数的和之差的最大值记为 $m_k(k=1,2, \cdots, 2 n+1)$. 将 $m_1, m_2, \cdots, m_{2 n+1}$ 中的最小值称为数列 $A_{2 n+1}$ 的特征值.
(1) 已知数列 $A_5: 1,2,3,3,3$, 写出 $m_1, m_2, m_5$ 的值及 $A_5$ 的特征值;
(2) 若 $x_1 \leqslant x_2 \leqslant \cdots \leqslant x_{2 n+1}$, 当 $[\mathrm{i}-(n+1)]\{j-(n+1)] \geqslant 0$, 其中 $\mathrm{i}, j \in\{1,2, \cdots, 2 n+1\}$, 且 $\mathrm{i} \neq j$ 时, 证.明: $\left|m_i-m_j\right|=\left|x_i-x_j\right|$;
(3) 已知数列 $A_{2 n+1}$ 的特征值为 $n-1$, 求 $\sum_{j>i \ge 1}^{i < j < 2 n+1}\left|x_i-x_j\right|$ 的最小值.