单选题 (共 6 题 ),每题只有一个选项正确
已知平面内有 e $O$ 和点 $A, B$, 若e $O$ 半径为 $2 \mathrm{~cm}$, 线段 $O A=3 \mathrm{~cm}, O B=2 \mathrm{~cm}$, 则直线 $A B$ 与 e $O$ 的位置关系为 ( )
$\text{A.}$ 相离
$\text{B.}$ 相交
$\text{C.}$ 相切
$\text{D.}$ 相交或相切
如图, 四边形 $A B C D$ 内接于 $\odot O, A B=C D, A$ 为 $\widehat{B D}$ 中点, $\angle B D C=60^{\circ}$, 则 $\angle A D B$ 等于 ( )
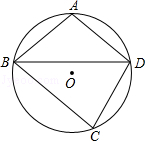
$\text{A.}$ $40^{\circ}$
$\text{B.}$ $50^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $70^{\circ}$
如图, $A$ 是 $\odot O$ 上一点, $B C$ 是直径, $A C=2, A B=4$, 点 $D$ 在 $\odot O$ 上且平分 $\widehat{B C}$, 则 $D C$ 的 长为 ( )
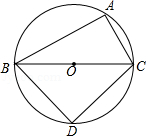
$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ $2 \sqrt{5}$
$\text{D.}$ $\sqrt{10}$
如图, $A B$ 为 $\odot O$ 的直径, 点 $P$ 在 $A B$ 的延长线上, $P C, P D$ 与 $\odot O$ 相切, 切点分别为 $C, D$. 若 $A B=6, P C=4$, 则 $\sin \angle C A D$ 等于( )
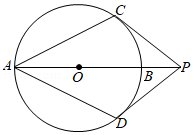
$\text{A.}$ $\frac{3}{5}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{4}{5}$
如图, 点 $A, B, C, D, E$ 在圆 $\mathrm{O} \|$ 上, $A B=C D, \angle A O B=42^{\circ}$, 则 $\angle C E D=()$
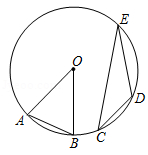
$\text{A.}$ $48^{\circ}$
$\text{B.}$ $24^{\circ}$
$\text{C.}$ $22^{\circ}$
$\text{D.}$ $21^{\circ}$
如图, $A B$ 是 $\odot O$ 的直径, 点 $C$ 为圆上一点, $A C=3, \angle A B C$ 的平 分线交 $A C$ 于点 $D, C D=1$, 则 $\odot O$ 的直径为
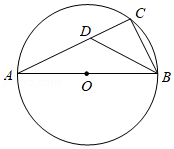
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ 1
$\text{D.}$ 2