单选题 (共 16 题 ),每题只有一个选项正确
设集合 $A=\{-2,-1,0,1,2\}, B=\left\{x \left\lvert\, 0 \leq x < \frac{5}{2}\right.\right\}$ ,则 $A \cap B=(\quad)$
$\text{A.}$ $\{0,1,2\}$
$\text{B.}$ $\{-2,-1,0\}$
$\text{C.}$ $\{0,1\}$
$\text{D.}$ $\{1,2\}$
设全集 $U=\{-2,-1,0,1,2,3\}$ ,集合 $A=\{-1,2\}, B=\left\{x \mid x^2-4 x+3=0\right\}$ ,则 $C_U(A \cup B)=$
$\text{A.}$ $\{1,3\}$
$\text{B.}$ $\{0,3\}$
$\text{C.}$ $\{-2,1\}$
$\text{D.}$ $\{-2,0\}$
集合 $M=\{2,4,6,8,10\}, N=\{x \mid-1 < x < 6\}$ ,则 $M \cap N=(\quad)$
$\text{A.}$ $\{2,4\}$
$\text{B.}$ $\{2,4,6\}$
$\text{C.}$ $\{2,4,6,8\}$
$\text{D.}$ $\{2,4,6,8,10\}$
设全集 $U=\{1,2,3,4,5\}$ ,集合 $M$ 满足 $C_U M=\{1,3\}$ ,则( )
$\text{A.}$ $2 \in M$
$\text{B.}$ $3 \in M$
$\text{C.}$ $4 \notin M$
$\text{D.}$ $5 \notin M$
若集合 $M=\left\{x_{\mid} \sqrt{x} < 4\right\}, \quad N=\left\{x_{\mid} 3 x \geq 1\right\}$ ,则 $M \cap N=(\quad)$
$\text{A.}$ $\{x \mid 0 \leq x < 2\}$
$\text{B.}$ $\left\{x \left\lvert\, \frac{1}{3} \leq x < 2\right.\right\}$
$\text{C.}$ $\{x \mid 3 \leq x < 16\}$
$\text{D.}$ $\left\{x \left\lvert\, \frac{1}{3} \leq x < 16\right.\right\}$
已知集合 $A=\{-1,1,2,4\}, B=\{x| | x-1 \mid \leq 1\}$ ,则 $A \cap B=(\quad)$
$\text{A.}$ $\{-1,2\}$
$\text{B.}$ $\{1,2\}$
$\text{C.}$ $\{1,4\}$
$\text{D.}$ $\{-1,4\}$
已知集合 $A=\{0,1,2,3,4,5,6\}, B=\{2,4,6,8\}$ ,则 $A \cap B=(\quad)$
$\text{A.}$ $\{2,4,6,8\}$
$\text{B.}$ $\{2,4,6\}$
$\text{C.}$ $\{0,1,2,3,4,5,6,8\}$
$\text{D.}$ $\{2,4\}$
已知集合 $A=\{x \mid 1 \leq x \leq 3\}, B=\{x \mid 2 < x < 4\}$ ,则 $A \cap B=$
$\text{A.}$ 2,3
$\text{B.}$ 1,4$)$
$\text{C.}$ $(-\infty, 4)$
$\text{D.}$ $1,+\infty)$
设集合 $M=\{x \mid-1 < x < 1\}, N=\{x \mid x(x-2) \leq 0\}$ ,则 $M \cap N=$
$\text{A.}$ $-1,2$
$\text{B.}$ $-1,0$
$\text{C.}$ $(0,1)$
$\text{D.}$ 0,2
已知集合 $A=\{x \mid x(x-5) < 0\}, B=\{x \mid x>2\}, M=A \cap B$ ,则( )
$\text{A.}$ $4 \notin M$
$\text{B.}$ $\sqrt{10} \in M$
$\text{C.}$ $5 \in M$
$\text{D.}$ $6 \in M$
已知集合 $A=\{(x, y) \mid x-y=0\}, B=\{(x, y) \mid x+y+1=0\}$ ,则 $A \cap B$ 的子集个数为( )
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 无穷多个
设集合 $A, B, C$ 均为非空集合.( )
$\text{A.}$ 若 $A \cap B=B \cap C$ ,则 $A=C$
$\text{B.}$ 若 $A \cup B=B \cup C$ ,则 $A=C$
$\text{C.}$ 若 $A \cap B=B \cup C$ ,则 $C \subseteq B$
$\text{D.}$ 若 $A \cup B=B \cap C$ ,则 $C \subseteq B$
如图,三个圆的内部区域分别代表集合A,B,C,全集为I,则图中阴影部分的区域表示
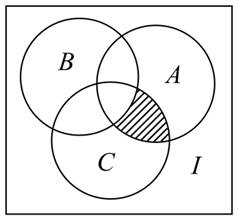
$\text{A.}$ $A \cap B \cap C$
$\text{B.}$ $A \cap C \cap\left(C_I B\right)$
$\text{C.}$ $A \cap B \cap\left(C_I C\right)$
$\text{D.}$ $B \cap C \cap\left(C_I A\right)$
设集合 $A=\left\{x \mid x^2 \geq 1\right\}, B=\{x \mid-1 < x < 2\}$ ,则 $A \cap B=(\quad)$
$\text{A.}$ $\{x \mid x>-1\}$
$\text{B.}$ $\{x \mid x \geq-1\}$
$\text{C.}$ $\{x \mid-1 < x < 1\}$
$\text{D.}$ $\{x \mid 1 \leq x < 2\}$
已知集合 $A=\left\{x \mid 2^x < 4\right\}, B=\left\{x \mid-2 < \log _2 x < 2\right\}$ ,则 $A \cap B=(\quad)$
$\text{A.}$ $\left\{x \left\lvert\, \frac{1}{4} < x < 4\right.\right\}$
$\text{B.}$ $\left\{x \left\lvert\, \frac{1}{4} < x < 2\right.\right\}$
$\text{C.}$ $\{x \mid 2 < x < 4\}$
$\text{D.}$ $\{x \mid 1 < x < 2\}$
已知集合 $A=\left\{x \mid x^2-7 x+12 \leq 0\right\}, B=\{x \mid 2 x+m>0\}$ ,若 $A \subseteq B$ ,则 $m$ 的取值范围为( )
$\text{A.}$ $(-6,+\infty)$
$\text{B.}$ $-6,+\infty)$
$\text{C.}$ $(-\infty,-6)$
$\text{D.}$ $-\infty,-6$
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知集合 $A=\{x \mid a \leqslant x \leqslant a+3\}, B=\left\{x \mid x^2+x-6 \leqslant 0\right\}$ .
(1)当 $a=0$ 时,求 $A \cup B, A \cap\left( C _{ R } B\right)$ ;
(2)若 $A \cap B=A$ ,求实数 a 的取值范围.
已知集合 $A=\{1,3, \sqrt{x}\}, B=\{2-x, 1\}$ .
(1)记集合 $M=\{1,4, y\}$ ,若集合 $A=M$ ,求实数 $x+y$ 的值;
(2)是否存在实数 $x$ ,使得 $B \subseteq A$ ?若存在,求出 $x$ 的值;若不存在,请说明理由.