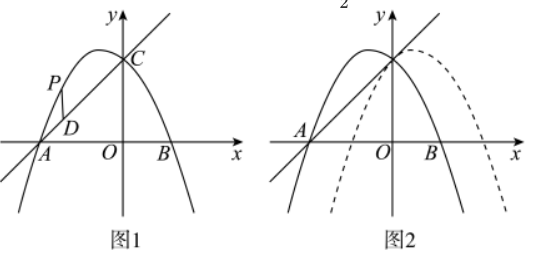
如图1，在平面直角坐标系中，抛物线 $y=-\frac{1}{2} x^2-x+4$ 与 $x$ 轴分别交于 $A, B$ 两点 (点 $A$ 在点 $B$ 左侧)，与 $y$ 轴交于 $C$ 点.

(1)求 $\triangle A B C$ 的面积;
(2)点 $P$ 为直线 $A C$ 上方抛物线上的任意一点，过点 $P$ 作 $P D \| y$ 轴交直线 $A C$ 于点 $D$ ，求 $P D+\frac{\sqrt{2}}{2} C D$ 的最大值及此时点 $P$ 的坐标; (3)如图 2 ，将抛物线沿着水平方向向右平移 2 个单位长度得到新的抛物线，点 $E$ 为原抛物线与平移后的抛物线的交点，点 $M$ 为平移后的抛物线对称轴上的一动点，点 $N$ 为坐标平面内的一点，直接写出所有使得以点 $B 、 E 、 M 、 N$ 为顶点的四边形是菱形的点 $\mathrm{N}$ 的坐标，并把求其中一个点 $N$ 的坐标的求解过程写出来.