利用正方形纸片的折叠开展数学活动, 探究体会在正方形折叠过程中, 图形与线段的变化及其蕴含的数学思想方法.

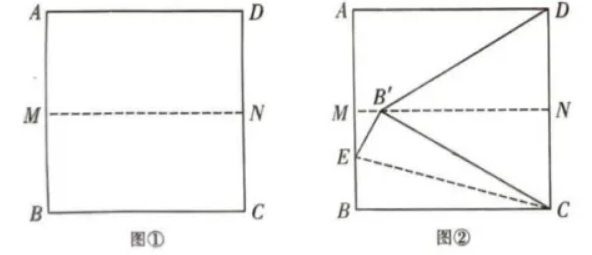
如图 ①,E 为正方形 $A B C D$ 的 $A B$ 边上的一个动点, $A B=6$, 将正方形 $A B C D$ 对折, 便点 $A$ 与点 $B$ 重合, 点 $C$ 与点 $D$ 重合, 折痕为 $M N$.
思考探索
(1) 将正方形 $A B C D$ 展平后沿过点 $C$ 的直线 $C E$ 折叠, 使点 $B$ 的对应点 $B^{\prime}$ 落在 $M N$ 上, 折痕为 $E C$, 连接 $D B^{\prime}$, 如图 (2), 请根据以上条件填空.
①点 $B^{\prime}$ 在以点 $E$ 为圆心, $\qquad$的长为半径的圆上(填线段);
②$B^{\prime} M$ 的长为 $\qquad$

拓展延伸

(2) 当 $A E=2$ 时, 正方形 $A B C D$ 沿过点 $E$ 的直线 $l$ (不过点 B) 折叠后, 点 $B$ 的对应点 $\mathrm{B}^{\prime}$ 落在正方形 $A B C D$ 的内部或边上.
① 求 $\triangle A B B^{\prime}$ 面积的最大值;
②连接 $A B^{\prime}, P$ 为 $A E$ 的中点, 点 $Q$ 在 $A B^{\prime}$ 上,连接 $P Q, \angle A Q P=\angle A B^{\prime} E$, 求 $B^{\prime} C+2 P Q$的最小值.