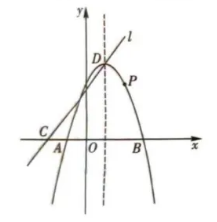
如图,拋物线 $y=-x^2+b x+c$ 与 $x$ 轴相交于 $A, B$ 两点 (点 $A$ 在点 $B$ 的左侧), 顶点 $D(1,4)$ 在直线 $l : y=\frac{4}{3} x+t$ 上,动点 $P$ 在抛物线上.
（1）求这条抛物线对应的函数表达式，
(2) 直线 $l$ 交 $x$ 轴于点 $C$, 则点 $C$ 的坐标为 $\qquad$ '
(3) 设点 $P$ 的横坐标为 $m$, 当 $1 < m < 3$ 时, 求四边形 $D C B P$ 面积的最大值;
(4) 设直线 $A P, B P$ 与抛物线的对称轴分别相交于点 $E, F$, 点 $G$ 为点 $E$ 关于 $x$ 轴的对称点, 请探索四边形 $A F B G$ 的面积是否随着点 $P$ 的运动而发生变化? 若不变, 求出这个四边形的面积; 若变化,说明理由.