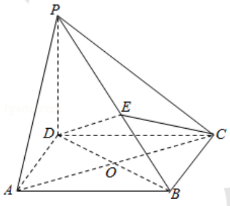
如图, 在四棱锥 $P-A B C D$ 中, $P D \perp$ 平面 $A B C D$, 四边形 $A B C D$ 是菱形, $A C=2, B D=2 \sqrt{3}$, 且 $A C, B D$ 交于点 $O, E$ 是 $P B$ 上任意一点.
(1) 求证: $A C \perp D E$;
(2) 若 $E$ 为 $P B$ 的中点, 且二面角 $A-P B-D$ 的余弦值为 $\frac{\sqrt{21}}{7}$, 求 $E C$与平面 $P A B$ 所成角 $\theta$ 的正弦值.