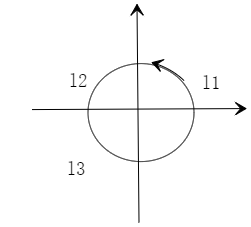
设曲线 $L$ 为 $x^2+y^2=1$, 取逆时针方向, $f(x, y)>0, f(x,-y)=f(x, y) \cdot L_1, L_2, L_3$ ,如图所示,记 $I_1=\int_{L_1} f(x, y) d x, I_2=\int_{L_2} f(x, y) d s, \quad I_3=\int_{L_3} f(x, y) d x$ ,则
A
$I_1>I_2>I_3$
B
$ I_2>I_3>I_1$.
C
$ I_3>I_2>I_1$
D
$I_2>I_1>I_3$
E
F