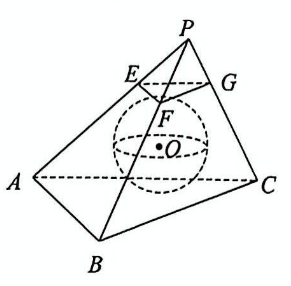
如图, 在三棱锥 $P-A B C$ 中, $P A=P B=C A=C B=2, \angle A P B=$ $\angle A C B=\frac{\pi}{2}, E, F, G$ 分别为 $P A, P B, P C$ 上靠近点 $P$ 的三等分点, 若此时恰好存在一个小球与三棱锥 $P-A B C$ 的四个面均相切, 且小球同时还与平面 $E F G$ 相切, 则 $P C=$
A
$\sqrt{6}+\sqrt{2}$
B
$\sqrt{6}-\sqrt{2}$
C
$\sqrt{13}+1$
D
$\sqrt{13}-1$
E
F