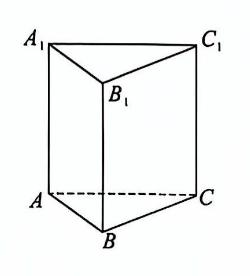
甲同学想用一支铅笔从如下的直三棱柱的顶点 $C_1$ 出发沿三棱柱的棱逐步完成"一笔画", 即每一步均沿着某一条棱从一个端点到达另一个端点, 紧接着从上一步的终点出发随机选择下一条棱再次画出,进而达到该棱的另一端点,按此规律一直进行,其中每经过一条棱称为一次移动,并随机选择某个顶点处停止得到一条"一笔画"路径,比如 "一笔画"路径 $C_1 \rightarrow B_1 \rightarrow A_1 \rightarrow A \rightarrow C$ 。若某"一笔画"路径中没有重复经过任何一条棱,则称该路径为完美路径,否则为不完美路径.下列说法正确的有
A
若"一笔画"路径为完美路径,则甲不可能 6 次移动后回到点 $C_1$
B
经过 4 次移动后仍在点 $C_1$ 的概率为 $\frac{19}{81}$
C
若"一笔画"路径为完美路径,则 5 次移动后回到点 $C_1$ 有 5 条不同笔迹
D
经过 3 次移动后, 到达点 $A_1$ 的条件下经过点 $C$ 的概率为 $\frac{1}{3}$
E
F