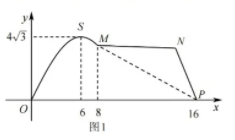
如图 1 , 某市拟在长为 16 km 的道路 $O P$ 的一侧修建一条运动赛道, 赛道的前一部分为曲线段 $O S M$, 该曲线段为函数 $y=A \sin \omega x(A>0, \omega>0), x \in[0,8]$ 的图象, 且图象的最高点为 $S(6,4 \sqrt{3})$ ；赛道的后一部分为折线段 $M N P$, 为保证参赛运动员的安全, 限定 $\angle M N P=120^{\circ}$.
(1) 求 $A, \omega$ 的值和 $M, P$ 两点间的距离;
(2) 若 $N P=\frac{\sqrt{3}-1}{2} M N$, 求折线段赛道 $M N P$ 的长度.