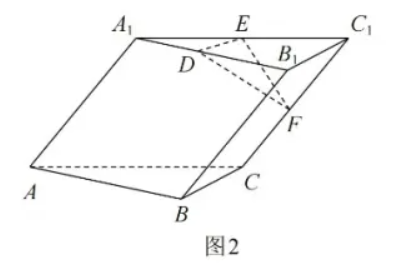
如图 2, 在三棱柱 $A B C-A_1 B_1 C_1$ 中, 侧面 $A C C_1 A_1$ 为菱形, $\angle A_1 A C=60^{\circ}$, 底面 $A B C$ 为等边三角形, 平面 $A C C_1 A_1 \perp$ 平面 $A B C$, 点 $D, E$ 满足 $\overrightarrow{A_1 D}=\frac{1}{3} \overrightarrow{A_1 B_1}, \overrightarrow{A_1 E}=\frac{1}{2} \overrightarrow{A_1 C_1}$, 点 $F$ 为棱 $C_1 C$ 上的动点 (含端点).
(1) 当 $F$ 与 $C$ 重合时, 证明: 平面 $D E F \perp$ 平面 $A B C$;
(2) 是否存在点 $F$, 使得直线 $A C$ 与平面 $D E F$ 所成角的正弦值为 $\frac{\sqrt{6}}{4}$ ? 若存在, 求出 $\frac{C_1 F}{C_1 C}$ 的值.