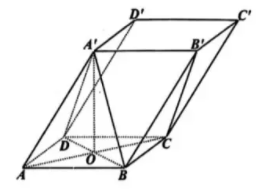
如图，在平行六面体 $A B C D-A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ 中，$A B=A D=2, \angle A^{\prime} A B=\angle A^{\prime} A D$ ，且 $A^{\prime} B \perp A C$ ，设 $A C$ 与 $B D$ 的交于点 $O$ ．
（1）证明：$A^{\prime} O \perp$ 平面 $A B C D$ ；
（2）若 $A A^{\prime}=3$ ，且 $\angle B A D=60^{\circ}$ ，求直线 $A^{\prime} B$ 与平面 $A^{\prime} B^{\prime} C D$ 所成角的正弦值．