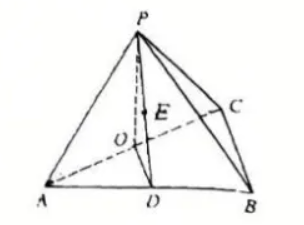
如图．在三棱锥 $P-A B C$ 中．，侧面 $P A C$ 为等腰三角形，$\angle A P C=\frac{2 \pi}{3}, O$ 为 $A C$ 的中点．$D$ 为 $A B$ 的中点．$O P=O D=1 . A B=4$ ，点 $E$ 在 $P D$ 上 ．
（1）若 $2 \overrightarrow{P E}=\overrightarrow{P D}$ ，证明，平面 $A C E \perp$ 平面 $P A B$ ．
（2）若 $P B=2 \sqrt{2}$ ，求平而 $P A B$ 与平面 $P B C$ 夹角的余弦值
$\text{A.}$
$\text{B.}$
$\text{C.}$
$\text{D.}$
$\text{E.}$
$\text{F.}$