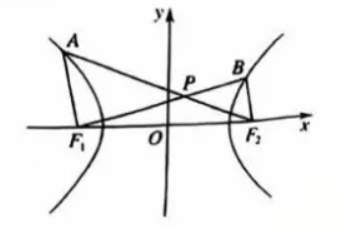
如图，已知 $F_1, F_2$ 为双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左，右焦点，直线 $y=\frac{\sqrt{2}}{2} x$ 为 $C$ 的一条渐近线，$A, B$ 分别为 $C$ 上位于第二，一象限内的点，$A F_1, B F_2$ 的倾斜角分别为 $\theta_1, \theta_2$ ，且当 $\theta_1=\frac{\pi}{2}$时，$\left|A F_1\right|=\frac{\sqrt{2}}{2}$ ．
（1）求双曲线 $C$ 的标准方程．
（2）若 $\theta_1=\theta_2$ ，连接 $A F_2, B F_1$ 相交于 $P$ ．
（i）若 $\left|A F_1\right|-2=\left|B F_2\right|$ ，求直线 $B F_2$ 的方程．
（ii）证明：点 $P$ 在以 $F_1, F_2$ 为焦点的椭图上，并求出该椭圆的标准方程．