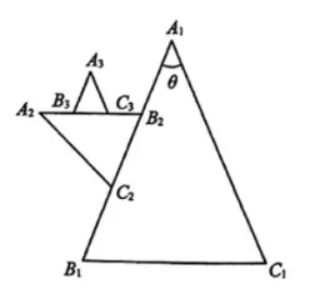
如图，已知给定线段 $B_1 C_1$ 长为 2 ，以 $B_1 C_1$ 为底边作顶角为 $\theta\left(0^{\circ} < \theta \leq 90^{\circ}\right)$ 的等腰三角形 $A_1 B_1 C_1$ ，取 $\triangle A_1 B_1 C_1$ 的腰 $A_1 B_1$ 的三等分点 $B_2, C_2\left(B_2\right.$ 靠近 $\left.A_1\right)$ ，以 $B_2 C_2$ 为底边向 $\triangle A_1 B_1 C_1$ 外部作顶角为 $\theta$ 的等腰三角形 $A_2 B_2 C_2 \cdots \cdots$ 依次类推，取 $\triangle A_{n-1} B_{n-1} C_{n-1}$ 的腰 $A_{n-1} B_{n-1}$ 的三等分点 $B_n, C_n\left(B_n\right.$ 靠近 $\left.A_{n-1}\right)$ ，以 $B_n C_n$ 为底边向 $\triangle A_{n-1} B_{n-1} C_{n-1}$ 外部作顶角为 $\theta$ 的等腰三角形 $A_n B_n C_n(n \geq 2)$ ，得到三角形列 $\left\{\triangle A_n B_n C_n\right\}$ ．
（1）用 $\theta$ 表示出 $\triangle A_2 B_2 C_2$ 的外接圆半径；
（2）当 $\theta=60^{\circ}$ 时，证明：$\left\{\triangle A_n B_n C_n\right\}$ 各顶点均在 $\triangle A_1 B_1 C_1$外接圆上或其内部；
（3）若 $\left\{\triangle A_n B_n C_n\right\}$ 各顶点均在 $\triangle A_1 B_1 C_1$ 外接圆上或其内部，求 $\cos \theta$ 的取值范围．