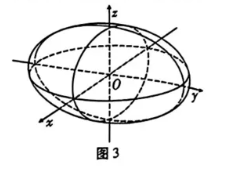
在空间直角坐标系下，由方程 $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1(a>0, b>0, c>0$ ，且 $a, b, c$ 不全相等 $)$所确定的曲面称为椭球面，若用坐标平面 $x=0, y=0, z=0$ 分别截椭球面，所得的截面是圆或者椭圆（如图3所示），这三个截面的方程分别为：$\left\{\begin{array}{l}\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 \\ x=0\end{array},\left\{\begin{array}{l}\frac{x^2}{a^2}+\frac{z^2}{c^2}=1 \\ y=0\end{array},\left\{\begin{array}{l}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\ z=0\end{array}\right.\right.\right.$ ．已知方程：$\frac{x^2}{12}+$ $\frac{y^2}{9}+\frac{z^2}{4}=1$ 所确定的椭球面分别交 $x$ 轴，$y$ 轴，$z$ 轴的正半轴于点 $A, ~ B, ~ C$ ．椭圆 $\tau$ 的方程为：$\left\{\begin{array}{l}\frac{x^2}{12}+\frac{y^2}{9}+\frac{z^2}{4}=1 \\ y=1\end{array}\right.$ ，若动点 $P$在椭圆 $\tau$ 上运动，则三棱锥 $P-A B C$ 体积的最大值为