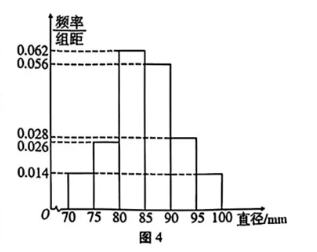
已知某种业公司培育了新品种的橙子，现从某批次收获的果实中随机抽取了 100 个橙子（直径位于 70 mm 至 100 mm 之间）作为样本，统计得到如图 4 所示的频率分布直方图．
（1）根据长期检测结果发现橙子直径服从正态分布，并将直径 $\geqslant 90 mm$ 的橙子定为特级品．此批次样本橙子直径的标准差 $s \approx 5 mm$ ，用标准差 $s$ 作为 $\sigma$ 的估计值，用样本平均数 $\bar{x}$ 作为 $\mu$ 的近似值．现从该批次中任取一个，试估计该橙子为特级品的概率 （保留小数点后两位数字）；（同一组中的数据用该组区间的中点值代表）
（2）在样本中，从直径在区间［85，90）， $[90,95),[95,100)$ 上的橙子中利用按比例分配

图4样本的分层抽样随机抽取 7 个橙子进行检测，再从中抽取 3 个橙子作进一步检测．记这 3 个橙子中直径在区间 $[90,95)$ 上的个数为 $X$ ，求 $X$ 的分布列与数学期望．
附参考数据：若随机变量 $\xi$ 服从正态分布 $N\left(\mu, \sigma^2\right)$ ，则 $P(\mu-\sigma \leqslant \xi \leqslant \mu+\sigma) \approx 0.6827$ ， $P(\mu-2 \sigma \leqslant \xi \leqslant \mu+2 \sigma) \approx 0.9545, P(\mu-3 \sigma \leqslant \xi \leqslant \mu+3 \sigma) \approx 0.9973$ ．