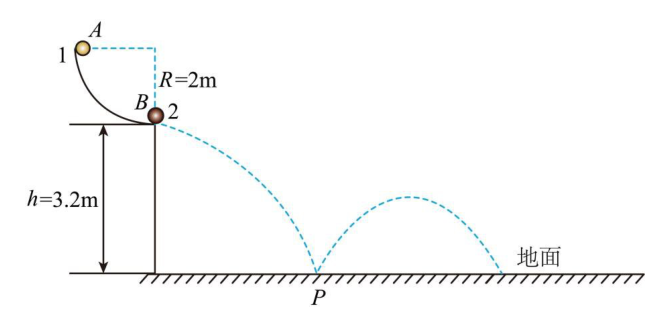
如图所示，四分之一坚直圆弧轨道 $A B$ 的半径 $R=2 m$ 。现有一质量 $m_0=0.4 kg$ 的小球 1 从 $A$ 点无初速度释放，沿圆弧轨道下滑到 $B$ 点与质量 $m=0.2 kg$ 的小球 2 发生弹性正碰，碰撞后小球 2 水平飞离轨道，落到水平地面上的 $P$ 点。小球 2 与地面碰撞后弹起（部分轨迹如图所示），多次碰撞后最终静止。假设小球 2 每次与地面碰撞机械能损失 $75 \%$ ，碰撞前后速度方向与地面间的夹角相等，碰撞过程中，小球 2 所受地面水平方向的作用力为坚直方向作用力的 $k$（未知）倍。小球 1 落地后被锁定，小球 1,2 均可以视为质点，碰撞时间极短，不计空气阻力。已知小球 1 沿圆弧轨道下滑时克服摩擦力做功为 $6.2 J, P 、 B$ 两点间的高度差为 3.2 m ，小球 2 第一次与地面碰撞的时间 $\triangle t=0.1 s$ 。 g 取 $10 m / s ^2$ 。求：［（2）（3）问结果可用分数表示］



（1）两球碰撞后瞬间，轨道对小球 2 的支持力大小；
（2）$k$ 的数值；
（3）小球 2 从 $B$ 点飞出到静止所发生的水平位移。