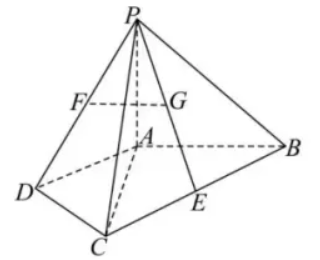
四棱锥 $P-A B C D$ 中，$\triangle A C D$ 与 $V A B C$ 为等腰直角三角形，$\angle A D C=90^{\circ}, \angle B A C=90^{\circ}$ ， $E$ 为 $B C$ 的中点．
（1）$F$ 为 $P D$ 的中点，$G$ 为 $P E$ 的中点，证明：$F G / /$ 平面 $P A B$ ；
（2）若 $P A \perp$ 平面 $A B C D, P A=A C$ ，求 $A B$ 与平面 $P C D$ 所成角的正弦值．