21．［项目主题］
某劳动实践小组拟用正三角形和正六边形两种环保组件改善小区幼儿园室内活动场地．
［项目准备］
（1）密铺知识学习：用形状、大小完全相同的一种或几种平面图形进行拼接，使图形之间既没有空隙也没有重叠地铺成一片，叫做图形的密铺．
（2）密铺方式构建：运用密铺知识得到图 1、图 2 所示的两种拼接方式，其中正六边形和正三角形组件的边长均为 20 cm ．
（3）密铺规律探究：为方便研究，称图3、图4分别为图1、图2的＂拼接单元＂．

观察发现：自左向右拼接图 1 时，每增加一个图 3 所示的拼接单元，则增加 1 个正六边形和 2个正三角形，长度增加 40 cm ，从而 x 个这样的拼接单元拼成一行的长度为 $(40 x +10) cm$ ．自左向右拼接图2时，每增加一个图4所示的拼接单元，则增加 $\qquad$ （1）个正六边形和 $\qquad$ （2）个正三角形，长度增加 $\qquad$ （3） cm ，从而 y 个这样的拼接单元拼成一行的长度为 $\qquad$ （4） cm ．
［项目分析］
（1）项目条件：场地为 $7.4 m \times 6 m$ 的矩形；正三角形和正六边形组件的单价分别为 1 元和 5 元．
（2）基本约定：项目成本仅计算所需组件的费用．
（3）方式确定：
（I）考虑成本因素，采用图 1 方式进行密铺；
（II）每行用正六边形组件顶着左墙开始，从左向右用一个正六边形与两个正三角形组件按图 1所示方式依次交替拼接，当不能继续拼接时，该行拼接结束；
（III）第一行紧靠墙边，从前往后按相同方式逐行密铺，直至不能拼接为止．
（4）方案论证：按上述确定的方式进行密铺，有以下两种方案．方案一：第一行沿着长度为 6 m 的墙自左向右拼接（如图5）．根据规律，令 $40 x+10 \leqslant 600$ ，解得 $x \leqslant 14.75$ ，所以每行可以先拼 14 块拼接单元，即共用去 14 个正六边形和 28 个正三



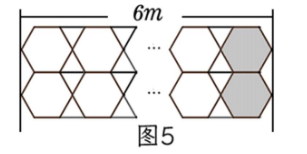
角形组件，由 $40 \times 14+10=570$ 知，所拼长度为 570 cm ，剩余 30 cm 恰好还可以摆放一个正六边形组件（如图5所示的阴影正六边形）．最终需用 15 个正六边形和 28 个正三角形组件，由 $5 \times 15+1 \times 28=103$ 知，方案一每行的成本为 103 元．由于每行宽度为 $20 \sqrt{ } 3 cm$（按 $\sqrt{ } 3=1.73$ 计算）设拼成 s 行，则 $20 \sqrt{3} s \leq 740$ ，解得 $s \leq \frac{37 \sqrt{3}}{3} \approx 21.34$ ，故需铺 21 行．由 $103 \times 21=2163$ 知，方案一所需的总成本为 2163 元．
方案二：第一行沿着长度为 7.4 m 的墙自左向右拼接．
类似于方案一的成本计算，令 $40 x+10 \leqslant 740 \ldots$
方案二每行的成本为 $\qquad$ （5）元，总成本为 (6) $\qquad$元
［项目实施］
根据以上分析，选用总成本较少的方案完成实践活动（略）．
请将上述材料中横线上所缺内容补充完整：