在 $\triangle A B C$ 中，$\angle A C B=90^{\circ}, \angle A B C=\alpha$ ，点 $D$ 在射线 $B C$ 上，连接 $A D$ ，将线段 $A D$ 绕点 A 逆时针旋转 $180^{\circ}-2 \alpha$ 得到线段 $A E$（点 $E$ 不在直线 $A B$ 上），过点 $E$ 作 $E F / / A B$ ，交直线 $B C$ 于点 $F$ ．

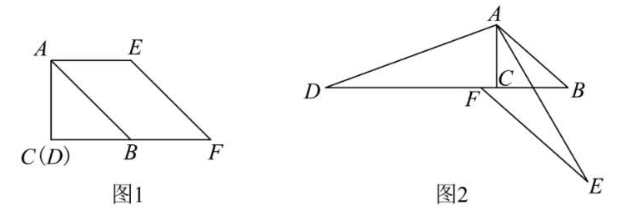
（1）如图 1，$\alpha=45^{\circ}$ ，点 $D$ 与点 $C$ 重合，求证：$B F=A C$ ；
（2）如图 2，点 $D, F$ 都在 $B C$ 的延长线上，用等式表示 $D F$ 与 $B C$ 的数量关系，并证明．