在平面直角坐标系 $x O y$ 中，对于点 A 和 $\odot C$ 给出如下定义：若 $\odot C$ 上存在两个不同的点 $M, N$ ，对于 $\odot C$ 上任意满足 $A P=A Q$ 的两个不同的点 $P, Q$ ，都有 $\angle P A Q \leq \angle M A N$ ，则称点 A 是 $\odot C$ 的关联点，称 $\angle M A N$ 的大小为点 A 与 $\odot C$ 的关联角度．（本定义中的角均指锐角、直角、钝角或平角）
（1）如图，$\odot O$ 的半径为 1 ．

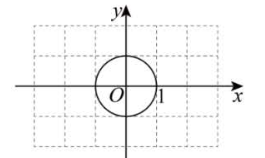
（1）在点 $A_1\left(\frac{1}{2}, 0\right), A_2\left(\frac{4}{3}, 0\right), A_3(2,0)$ 中，点 $\_\_\_\_$是 $\odot O$ 的关联点且其与 $\odot O$ 的关联角度小于 $90^{\circ}$ ，该点与 $\odot O$ 的关联角度为 $\_\_\_\_$ ${ }^{\circ}$ ；
（2）点 $B(1, m)$ 在第一象限，若对于任意长度小于 1 的线段 $B D, B D$ 上所有的点都是 $\odot O$ 的关联点，则 $m$ 的最小值为 $\_\_\_\_$ ；
（2）已知点 $E(1,3), F(4,3), T(t, 0), \odot T$ 经过原点，线段 $E F$ 上所有的点都是 $\odot T$ 的关联点，记这些点与 $\odot T$ 的关联角度的最大值为 $\alpha$ ．若 $90^{\circ} \leq \alpha \leq 180^{\circ}$ ，直接写出 $t$ 的取值范围．