已知椭圆 $\frac{x^2}{8}+\frac{y^2}{4}=1$ 的左、右焦点分别为 $F_1 、 F_2$ ，过坐标原点的直线交椭圆于 $A 、 B$ 两点，点 $A$ 在第一象限．


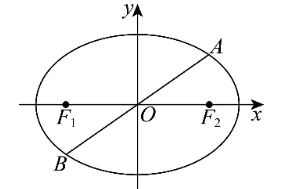
（1）若 $|O A|=\sqrt{6}$ ，求点 $A$ 的坐标；
（2）求 $\left|\overrightarrow{A F_1}+3 \overrightarrow{A F_2}\right|$ 的取值范围；
（3）若 $A E \perp x$ 轴，垂足为 $E$ ，连结 $B E$ 并延长交椭圆于点 $C$ ，求 $\triangle A B C$ 面积的最大值．