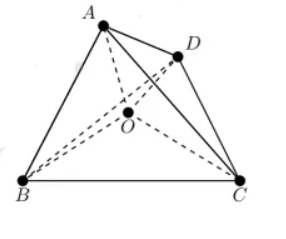
记三维欧氏空间中不共面的四点 $A, B, C, D$ 生成的四面体为 $A B C D$ ．在四面体 $A B C D$ 内部取一点 $O$ ，设四面体 $O B C D$ 的体积为 $V_A$ ，四面体 $O A C D$ 的体积为 $V_B$ ，四面体 $O A B D$ 的体积为 $V_C$ ，四面体 $O A B C$ 的体积为 $V_D$ ．
（1）求证：$(\overrightarrow{O A} \cdot(\overrightarrow{O C} \times \overrightarrow{O D}))(\overrightarrow{O B} \cdot(\overrightarrow{O C} \times \overrightarrow{O D})) < 0$ ；
（2）求证：$V_A \overrightarrow{O A}+V_B \overrightarrow{O B}+V_C \overrightarrow{O C}+V_D \overrightarrow{O D}=\overrightarrow{0}$ ．
$\text{A.}$
$\text{B.}$
$\text{C.}$
$\text{D.}$
$\text{E.}$
$\text{F.}$