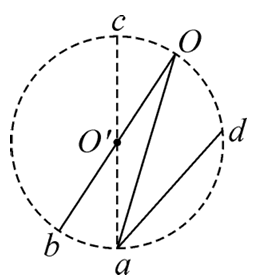
如图所示,$O a 、 O b$ 和 $a d$ 是坚直平面内三根固定的光滑细杆,$O$ 、 $a 、 b 、 c$ 、 $d$ 位于同一圆周上,$c$ 为圆周的最高点,$a$ 为最低点,$O^{\prime}$ 为圆心。每根杆上都套着一个小滑环(未画出),两个滑环从 $O$ 点无初速释放,一个滑环从 $d$ 点无初速释放,用 $t_1$ 、 $t_2 、 t_3$ 分别表示滑环沿 $O a 、 O b 、 d a$ 到达 $a 、 b$所用的时间,则下列关系正确的是
A
$t_1=t_2$
B
$t_2>t_3$
C
$t_1 < t_2$
D
$t_1=t_3$
E
F