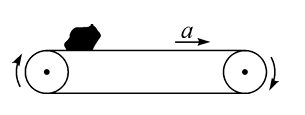
1.如图所示,一水平的浅色长传送带上放置一质量为 $m$ 的煤块(可视为质点),煤块与传送带的动摩擦因数为 $\mu$ 。初始时,传达带与煤块都是静止的。现让传送带以恒定的加速度 $a$ 开始运动,当其速度达到 $v$ 后,便以此速度做匀速运动。经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动,关于上述过程,以下判断正确的是(重力加速度为 $g$ )
A
$\mu$ 与 $a$ 之间一定满足关系 $\mu>\frac{a}{g}$
B
煤块从开始运动到相对于传送带静止经历的位移为 $\frac{v^2}{\mu g}$
C
煤块从开始运动到相对于传送带静止经历的时间为 $\frac{v}{\mu g}$
D
黑色痕迹的长度为 $\frac{v^2}{2 \mu g}$
E
F