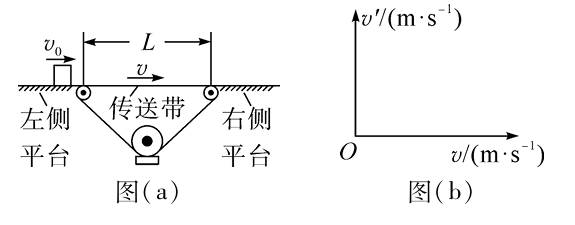
如图（a）所示，相距 $L=11.5 \mathrm{~m}$ 的两平台位于同一水平面内，二者之间用传送带相接。传送带向右匀速运动，其速度的大小 $v$ 可以由驱动系统根据需要设定。质量 $m=10 \mathrm{~kg}$的载物箱（可视为质点），以初速度 $v_0= 5.0 \mathrm{~m} / \mathrm{s}$ 自左侧平台滑上传送带。载物箱与传送带间的动摩擦因数 $\mu=0.10$ ，重力加速度取 $g=10 \mathrm{~m} / \mathrm{s}^2$ 。
（1）若 $v=4.0 \mathrm{~m} / \mathrm{s}$ ，求载物箱通过传送带所需的时间；
（2）求载物箱到达右侧平台时所能达到的最大速度和最小速度；
（3）在图（b）中大致画出载物箱离开传送带时的速度 $v^{\prime}$ 与传送带速度 $v$ 的关系图像，并标出图像拐点的坐标。