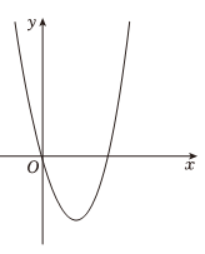
在平面直角坐标系中，点 $O$ 为坐标原点，抛物线 $y=x^2+b x$ 经过点 $(3,3)$ ，点 $A 、 B$ 是该抛物线上的两点，横坐标分别为 $m, m+1$ ，已知点 $M(1,1)$ ，作点 $A$ 关于点 $M$ 的对称点 $C$ ，作点 $B$ 关于点 $M$的对称点 $D$ ，构造四边形 $A B C D$ ．
（1）求该抛物线所对应的函数表达式；
（2）当 $A, B$ 两点关于该抛物线的对称轴对称时，求点 $C$ 的坐标；
（3）设抛物线在 $A 、 B$ 两点之间的部分（含 $A 、 B$ 两点）为图象 $G$ ，当 $0 < m < 1$ 时，若图象 $G$ 的最高点与最低点的纵坐标之差为 $\frac{1}{2}$ ，求 $m$ 的值；
（4）连结 $O A 、 O B$ ，当 $\angle A O B=\angle O A D+\angle O B C$ 时，直接写出 $m$ 的取值范围．（这里 $\angle A O B 、 \angle O A D 、 \angle O B C$ 均是大于 $0^{\circ}$ 且小于 $180^{\circ}$ 的角）