综合与探究
【探索发现】如图 1，小军用两个大小不同的等腰直角三角板拼接成一个四边形．
【抽象定义】以等腰三角形为边向外作等腰三角形，使该边所对的角等于原等腰三角形的顶角，此时该四边形称为＂双等四边形＂，原等腰三角形称为四边形的＂伴随三角形＂．如图 2，在 $\triangle A B C$ 中，$A B=A C$ ， $A C=A D, \angle D=\angle B A C$ ．此时，四边形 $A B C D$ 是＂双等四边形＂， $ \triangle A B C$ 是＂伴随三角形＂．


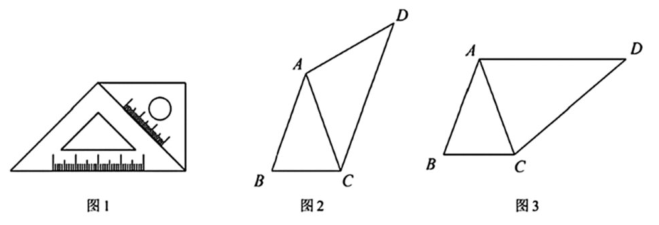
【问题解决】如图 3，在四边形 $A B C D$ 中，$A B=A C, A D=C D, \angle D=\angle B A C$ ．求：
① $A D$ 与 $B C$ 的位置关系为： $\_\_\_\_$ ：
② $A C^2$ $\_\_\_\_$ $A D \cdot B C$. （填＂＞＂，＂＜＂或＂＝＂）

【方法应用】 ① 如图4，将 $\mathrm{V} A B C$ 绕点 A 逆时针旋转至 $\mathrm{V} A D E$ ，点 $D$ 恰好落在 $B C$ 边上，求证：四边形 $A B D E$ 是双等四边形．

② 如图 5，在等腰三角形 $A B C$ 中，$A C=B C, \cos B=\frac{3}{5}, A B=5$ ，在平面内找一点 $D$ ，使四边形 $A B C D$是以 $\triangle A B C$ 为伴随三角形的双等四边形，若存在，请求出 $C D$ 的长，若不存在，请说明理由．