如图,在直四棱柱 $A B C D-A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ 中,底面 $A B C D$ 为菱形,且 $A A^{\prime}=2 A B=4$ , $\angle A B C=\frac{2 \pi}{3}$ ,若 $E$ 为棱 $A B$ 的中点,$F$ 为棱 $C C^{\prime}$ 上的动点(含端点),则下列说法正确的是
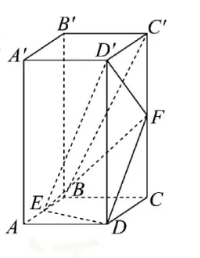
A
三棱锥 $D^{\prime}-D E F$ 的体积为定值
B
记直线 $E F$ 与平面 $D^{\prime} D E$ 所成的角为 $\theta$ ,则 $\sin \theta$ 的最大值为 $\frac{\sqrt{7}}{7}$
C
若 $C F=F C^{\prime}$ ,则异面直线 $D^{\prime} F$ 与 $B C^{\prime}$ 所成角的余弦值为 $\frac{3 \sqrt{10}}{20}$
D
若 $C F=F C^{\prime}$ ,则过 $D, E, F$ 三点的平面截该棱柱所得截面的面积为 $\frac{3 \sqrt{6}}{2}$
E
F