在平面直角坐标系中, 给出如下定义: $P$ 为图形 $M$ 上任意一点, 如果点 $P$ 到直线 $E F$ 的距离等于图形 $M$ 上任意两点距离的最大值时, 那么点 $P$ 称为直线 $E F$ 的“伴随点”.
例如: 如图 1, 已知点 $A(1,2), B(3,2), P(2,2)$ 在线段 $A B$ 上, 则点 $P$ 是直线 $E F: x$ 轴的“伴随点”.


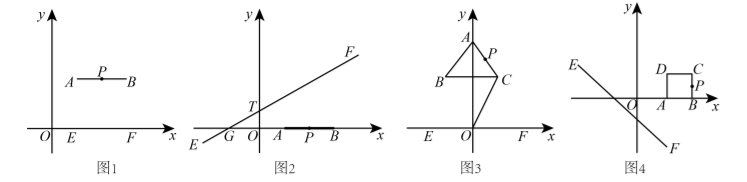
(1) 如图 2, 已知点 $A(1,0), B(3,0), P$ 是线段 $A B$ 上一点, 直线 $E F$ 过 $G(-1,0), T\left(0, \frac{\sqrt{3}}{3}\right)$ 两点, 当点 $P$ 是直线 $E F$ 的“伴随点”时, 求点 $P$ 的坐标;
(2) 如图 3, $x$ 轴上方有一等边三角形 $A B C, B C \perp y$ 轴, 顶点 $A$ 在 $y$ 轴上且在 $B C$ 上方, $O C=\sqrt{5}$, 点 $P$ 是 $\triangle A B C$ 上一点, 且点 $P$ 是直线 $E F: x$ 轴的“伴随点”. 当点 $P$ 到 $x$ 轴的距离最小时, 求等边三角形 $A B C$ 的 边长;
(3) 如图 4, 以 $A(1,0), B(2,0), C(2,1)$ 为顶点的正方形 $A B C D$ 上始终存在点 $P$, 使得点 $P$ 是直线 $E F$ : $y=-x+b$ 的“伴随点”. 请直接写出 $b$ 的取值范围.