综合与实践
(1)【思考尝试】
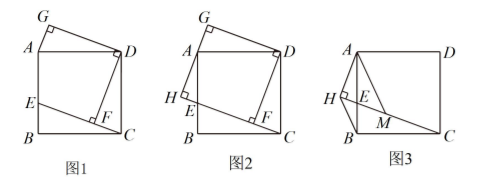
数学活动课上, 老师出示了一个问题: 如图 1, 在矩形 $\mathrm{ABCD}$ 中, $\mathrm{E}$ 是边 $A B$ 上一点, $D F \perp C E$ 于点 $\mathrm{F}, G D \perp D F$, $A G \perp D G, A G=C F$. 试猜想四边形 $A B C D$ 的形状, 并说明理由;
(2)【实践探究】
小䜭受此问题启发, 逆向思考并提出新的问题: 如图 2, 在正方形 $A B C D$ 中, $\mathrm{E}$ 是边 $A B$ 上一点, $D F \perp C E$ 于点 $\mathrm{F}, A H \perp C E$ 于点 $\mathrm{H}, G D \perp D F$ 交 $A H$ 于点 $\mathrm{G}$, 可以用等式表示线段 $F H, A H, C F$ 的数量关系, 请你 思考并解答这个问题;
(3)【拓展迁移】
小博深入研究小㕝提出的这个问题, 发现并提出新的探究点: 如图 3, 在正方形 $A B C D$ 中, $\mathrm{E}$ 是边 $A B$ 上一 点, $A H \perp C E$ 于点 $\mathrm{H}$, 点 $\mathrm{M}$ 在 $C H$ 上, 且 $A H=H M$, 连接 $A M, B H$, 可以用等式表示线段 $C M, B H$ 的数 量关系, 请你思考并解答这个问题.