单选题 (共 4 题 ),每题只有一个选项正确
如果实数 $a, b, c$ 在数轴上的位置如图所示, 那么代数式 $\sqrt{a^2}-|a+b|+\sqrt{(c-a)^2}+|b+c|$ 可以化简为
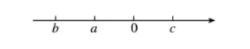
$\text{A.}$ $2 c a$
$\text{B.}$ 2 a 2 b
$\text{C.}$ a
$\text{D.}$ a
如果正比例函数 $y=a x(a \neq 0)$ 与反比例函数 $y=\frac{b}{x}(b \neq 0)$ 的图象有两个交点, 其中一个交点的坐标为 $(-3,-2)$, 那么另一个交点的坐标为 ( ).
$\text{A.}$ $(2,3)$
$\text{B.}$ $(3,-2)$
$\text{C.}$ $(-2,3)$
$\text{D.}$ $(3,2)$
如果 $a, b$ 为给定的实数, 且 $1 < a < b$, 那么 $1, a+1,2 a+b, a+b+1$ 这四个数据的平均数与中位数之差的绝对值是 ( ).
$\text{A.}$ 1
$\text{B.}$ $\frac{2 a-1}{4}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{1}{4}$
小倩和小玲每人都有若干面值为整数元的人民币. 小倩对小玲说: "你若给我 2 元, 我的钱数将是你的 n 倍";小玲对小倩说:"你若给我 n 元,我的钱数将是你的 2 倍",其中 n 为正整数,则 n 的可能值的个数是()。
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知二次函数 $y=x^2+(m+3) x+m+2$, 当 $-1 < x < 3$ 时, 恒有 $y < 0$; 关于 $x$ 的方程 $x^2+(m+3) x+m+2=0$ 的两个实数根的倒数和小于 $-\frac{9}{10}$. 求 $m$ 的取值范围.
已知整数 $a, b$ 满足: $a-b$ 是素数, 且 $a b$ 是完全平方数. 当 $a \geq 2012$ 时, 求 $a$ 的最小值。
求所有正整数 $n$, 使得存在正整数 $x_1, x_2, \cdots, x_{2012}$, 满足 $x_1 < x_2 < \cdots < x_{2012}$, 且
$$
\frac{1}{x_1}+\frac{2}{x_2}+\cdots+\frac{2012}{x_{2012}}=n
$$