解答题 (共 19 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
甲乙丙丁四人进行乒乓球双打练习,两人一对地结为对打的双方,有多少种不同的结对方式?
欲将 6 个人分为 3 组,每组 2 人,分别从事 3 项不同工作,求分配方式数.
要把 7 人分为 3 个小组,执行同一种任务,其中一个组 3 人,另两个组各 2 人,求分组方式数.
一批产品有 $N$ 个,其中废品有 $M$ 个。现从中随机取出 $n$ 个,在以下两种情形下,分别求 "其中恰好有 $m$ 个废品"这一事件的概率。
(1)有放回地选取;
(2)不放回地选取
$n$ 个男生,$m$ 个女生排成一排 $(m \leq n+1)$ .求事件 $A=\{$ 任意两个女孩不相邻 $\}$ 的概率。又若排成一圈,又如何?
$r$ 个不同的球任意放入编号为 1 至 $n$ 的 $n$ 个盒子,每球入各盒均等可能,求下列事件的概率
(1)$A=\{$ 指定的 $r$ 个盒子各含一个球 $\}$
(2)$B=\{$ 每盒至多有一球 $\}$
(3)$C=\{$ 某指定盒中恰有 $m$ 个球 $\}$
设有方程 $x+y+z=15$ ,试分别求出它的正整数解和非负整数解 $(x, y, z)$ 的组数.
设有 $n$ 个人随机地坐到礼堂第一排 $N$ 个座位上去,试求下列事件的概率:(1)任何人都没有邻座;(2)每人恰有一个邻座;(3)关于中央座位对称的两个座位至少有一个空着。
罐中放有 7 个白球和 3 个黑球,从中无放回地随机抽取 3 个球.已知其中之一是黑球,试求其余二球都是白球的概率
将 $n$ 根短绳的 $2 n$ 个端头任意两两连接,试求恰好连成 $n$ 个圈的概率.
某工厂的第一,二,三号车间生产同一产品,产量各总占产量的 $\frac{1}{2}, \frac{1}{3}, \frac{1}{6}$ ,次品率分别为 $1 \%, 1 \%$ 和 $2 \%$ .现从该厂产品中随机抽取一件,试求该产品是次品的概率.
罐中放有 $a$ 个白球和 $b$ 个黑球,每次从罐中随机抽取一个球,并连同 $c$ 个同色球一起放回罐中,如此反复进行.试证明:在第 $n$ 次取球时取出白球的概率为 $\frac{a}{a+b}$ .
某种疾病的患病率为 $0.5 \%$ ,通过验血诊断该病的误诊率为 $5 \%$(即非患者中有 $5 \%$ 的人验血结果为阳性,患者中有 $5 \%$ 的人验血结果为阴性)。现知某人验血结果为阳性,试求他确患有此病的概率。
甲乙二人相互独立地各自抛掷一枚均匀的硬币,试求在分别批掷 $n$ 次之后,两人掷出的正面次数相等的概率。
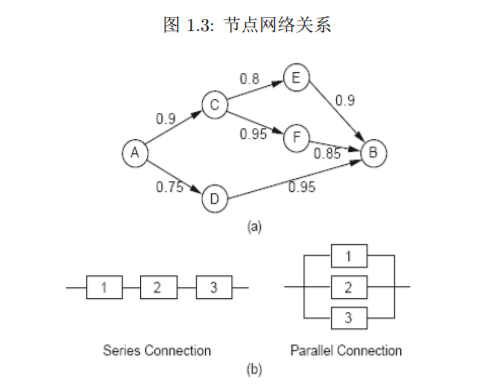
一个计算机网络上的节点 $A, B$ 通过节点 $C, D, E, F$ 连接起来,如图所示。假定任何两个直接相连的节点,记为 $i, j$ ,通路的概率是 $p_{i j}$ 。并假定任何两个连接失效是相互独立的。求 $A, B$ 是通路的概率。
口袋中有 $a$ 个黑球和 $b$ 个白球,他们除颜色不同外,其他方面没有任何区别。现把球随机的一个一个摸出来,求第 $k$ 次摸得一个黑球的概率。
一罐内有 $a$ 个黑球和 $b$ 个白球,从中任意取一球,如果是白球则将它放回去,如果是黑球,则从另一罐内取一白球替换它放回去。在重复 $n$ 次这样的做法后,求第 $n+1$ 次取出的是白球的概率。
参加集会的 $n$ 个人将他们的帽子放在一起,会后每人任取一顶帽子戴上.求恰有 $k$ 个人戴对自己的帽子的概率。
要给 $n$ 个单位发会议通知,由两个人分别在通知上写单位名称和写信封.如果写完之后,随机地把通知装入信封。试求下述各事件的概率:(1)恰有 $k$ 份通知装对信封;(2)至少有 $m$ 份通知装对信封。