单选题 （共 2 题 ），每题只有一个选项正确
下列不等式组是一元一次不等式组的是（ ）
$\text{A.}$ $\left\{\begin{array}{l}x+y=1 \\ x-y>1\end{array}\right.$
$\text{B.}$ $\left\{\begin{array}{l}x^2+x>2 \\ x+1>0\end{array}\right.$
$\text{C.}$ $\left\{\begin{array}{l}2 x+x>x \\ x+2>3 y\end{array}\right.$
$\text{D.}$ $\left\{\begin{array}{l}x+1 < 2 \\ 2 x+3>x-1 \\ x>2\end{array}\right.$
不等式组 $\left\{\begin{array}{l}x-2 < 0 \\ x \geqslant-1\end{array}\right.$ 的解集在数轴上表示正确的是 ．
$\text{A.}$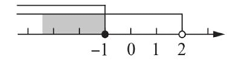 
$\text{B.}$ 
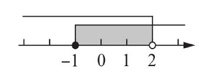$\text{C.}$ 
$\text{D.}$ 
解答题 （共 2 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
求不等式组 $-2 \leqslant \frac{1-2 x}{5}+1 \leqslant 6$ 的非负整数解．
某童装加工企业今年五月份，工人每人平均加工童装 150 套，最不熟练的工人加工的童装套数为平均套数的 $60 \%$ 。为了提高工人的劳动积极性，按照完成外商订货任务，企业计划从六月份起进行工资改革。改革后每位工人的工资分为两部分：一部分为每人每月基本工资 200元；另一部分为每加工 1 套童装奖励若干元。
（1）为了保证所有工人的每月工资收人不低于市有关部门规定的最低工资标准 450 元，按五月份工人加工的童装套数计算，工人每加工 1 套童装，企业至少应奖励多少元（精确到分）？
（2）根据经营情况，企业决定每加工 1 套童装奖励 5 元．工人小张争取六月份工资不少于1200 元，那么小张在六月份应至少加工多少套童装？