解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设
$$
f(x)=\left\{\begin{array}{cl}
1, & |x| < 1 \\
0, & |x|=1, g(x)=\mathrm{e}^x \\
-1, & |x|>1
\end{array}\right.
$$
求 $f[g(x)]$ 和 $g[f(x)]$, 并作出这两个函数的图形.
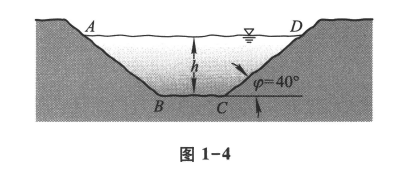
已知水渠的横断面为等腰梯形,斜角 $\varphi=40^{\circ}$ (图 1-4). 当过水断面 $A B C D$ 的面积为定值 $S_0$ 时, 求湿周 $L(L=A B+B C+C D)$ 与水深 $h$ 之间的函数关系式, 并指明其定义域.
设 $x O y$ 平面上有正方形 $D=\{(x, y)|0 \leqslant x \leqslant 1,0 \leqslant y \leqslant 1|$ 及直线 $l: x+y=t(t \geqslant 0)$.若 $S(t)$ 表示正方形 $D$ 位于直线 $l$ 左下方部分的面积, 试求 $S(t)$ 与 $t$ 之间的函数关系.
求联系华氏温度 (用 $F$ 表示) 和摄氏温度 (用 $C$ 表示) 的转换公式,并求
(1) $90{ }^{\circ} \mathrm{F}$ 的等价摄氏温度和 $-5^{\circ} \mathrm{C}$ 的等价华氏温度;
(2) 是否存在一个温度值, 使华氏温度计和摄氏温度计的读数是一样的? 如果存在,那么该温度值是多少?
已知 Rt $\triangle A B C$ 中, 直角边 $A C, B C$ 的长度分别为 20,15 , 动点 $P$ 从 $C$ 出发, 沿三角形边界按 $C \rightarrow B \rightarrow A$ 方向移动; 动点 $Q$ 从 $C$ 出发, 沿三角形边界按 $C \rightarrow A \rightarrow B$ 方向移动,移动到两动点相遇时为止, 且点 $Q$ 移动的速度是点 $P$ 移动的速度的 2 倍. 设动点 $P$ 移动的距离为 $x, \triangle C P Q$ 的面积为 $y$, 试求 $y$ 与 $x$ 之间的函数关系.