填空题 (共 9 题 ),请把答案直接填写在答题纸上
四边形 $A B C D$ 为矩形,$A B=\sqrt{2}, A D=3$ ,点 $E$ 为边 $B C$ 上一点,将 $\triangle D C E$ 沿 $D E$ 翻折,点 $C$ 的对应点为点 $F$ ,过点 $F$ 作 $D E$ 的平行线交 $A D$ 于点 $G$ ,交直线 $B C$ 于点 $H$ .若点 $G$ 是边 $A D$ 的三等分点,则 $F G$ 的长是
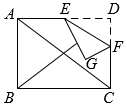
如图,四边形 $A B C D$ 为矩形,$A B=3, A D=4, A C, B D$ 为矩形的对角线,$E$ 是 $A D$ 边的中点,点 $F$ 是 $C D$上一点,连接 $E F$ ,将 $\triangle D E F$ 沿 $E F$ 折叠,当点 $G$ 落在矩形对角线上时,则折痕 $E F$ 的长是
在长为 2 ,宽为 $x(1 < x < 2)$ 的矩形纸片上,从它的一侧,剪去一个以矩形纸片宽为边长的正方形(第一次操作);从剩下的矩形纸片一侧再剪去一个以宽为边长的正方形(第二次操作);按此方式,如果第三次操作后,剩下的纸片恰为正方形,则 $x$ 的值为
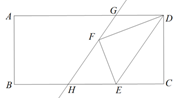
如图,将矩形纸片 $A B C D$ 折叠,折痕为 $M N$ ,点 $M, N$ 分别在边 $A D, B C$ 上,点 $C, D$ 的对应点分别在 $E$ , $F$ 且点 $F$ 在矩形内部,$M F$ 的延长线交 $B C$ 与点 $G, E F$ 交边 $B C$ 于点 $H . E N=2, A B=4$ ,当点 $H$ 为 $G N$ 三等分点时,$M D$ 的长为 $\qquad$ .
在矩形 $A B C D$ 中,$A B=9, A D=12$ ,点 $E$ 在边 $C D$ 上,且 $C E=4$ ,点 $P$ 是直线 $B C$ 上的一个动点.若 $\triangle A P E$是直角三角形,则 $B P$ 的长为
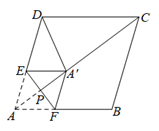
如图,已知在菱形 $A B C D$ 中,$A B=5, A C=8$ ,点 $P$ 是 $A C$ 上的一个动点,过点 $P$ 作 $E F \perp A C$ 交 $A D$ 于点 $E$ ,交 $A B$ 于点 $F$ ,将 $\triangle A E F$ 沿 $E F$ 折叠,使点 A 落在点 $A^{\prime}$ 处,当 $\triangle A^{\prime} C D$ 是直角三角形时,$A P$ 的长为 $\qquad$ .
已知,拋物线 $y=a x^2+2 a x+b$ 上有两点 $A(-2,4), B(1,0)$ ,将拋物线沿水平方向平移,平移后点 $A$ 的对应点为 $A^{\prime}$ ,点 $B$ 的对应点为 $B^{\prime}$ ,且四边形 $A A^{\prime} B^{\prime} B$ 刚好为菱形,那么平移后的抛物线的顶点坐标为
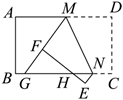
如图,在菱形 $A B C D$ 中,$\angle D A B=45^{\circ}, A B=4$ ,点 $P$ 为线段 $A B$ 上一动点,过点 $P$ 作 $P E \perp A B$ 交 $A D$ 于点 $E$ ,沿 $P E$ 将 $\angle A$ 折叠,点 A 的对称点为点 $F$ ,连接 $E F, ~ D F, ~ C F$ ,当 $\triangle C D F$ 为等腰三角形时,$A P$ 的长为 $\qquad$
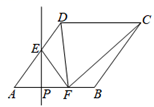
在矩形 $A B C D$ 中,$A D=5, A B=4$ ,点 $E, F$ 在直线 $A D$ 上,且四边形 $B C F E$ 为菱形,若线段 $E F$的中点为点 $M$ ,则线段 $A M$ 的长为 $\qquad$ .