单选题 (共 6 题 ),每题只有一个选项正确
设 $I_1=\iint_D(x+y) \operatorname{sgn}(x+y) \mathrm{d} x \mathrm{~d} y, I_2=\iint_D(x-y) \operatorname{sgn}(x-y) \mathrm{d} x \mathrm{~d} y$, 其中符号函数 $\operatorname{sgn} x=\left\{\begin{array}{l}1, x>0, \\ 0, x=0, \\ -1, x < 0,\end{array}\right.$ 区域 $D=\{(x, y) \mid-1 \leqslant x \leqslant 1,-1 \leqslant y \leqslant 1\}$, 则
$\text{A.}$ $I_1>I_2$
$\text{B.}$ $I_1 < I_2$
$\text{C.}$ $I_1=I_2$
$\text{D.}$ $I_1=-I_2$
设有向曲线 $L$ 上任一点 $(x, y)$ 处的切向量为 $(1,2 x)$, 则将 曲线积分 $\int_L P \mathrm{~d} x+Q \mathrm{~d} y$ 化为第一类曲线积分的结果为
$\text{A.}$ $\int_L(P+2 x Q) \mathrm{d} s$;
$\text{B.}$ $\int_L(2 x P+Q) \mathrm{d} s$;
$\text{C.}$ $\int_L \frac{P+2 x Q}{\sqrt{1+4 x^2}} \mathrm{~d} s$;
$\text{D.}$ $\int_L \frac{2 x P+Q}{\sqrt{1+4 x^2}} \mathrm{~d} s$.
若曲线积分 $\int_L x^2 y^2 \mathrm{~d} x+a x^3 y \mathrm{~d} y$ 的结果与路径无关, 则 $a=$.
$\text{A.}$ $\frac{3}{2}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ 2
设 $\Sigma$ 为曲面 $z=2-\left(x^2+y^2\right)$ 在 $x o y$ 平面上方的部分, 则 $I=\iint_{\Sigma} z d S=\begin{array}{ll}\quad \end{array}$
$\text{A.}$ $\int_1^{2 \pi} d \theta \int_0^{2-r^2}\left(2-r^2\right) \sqrt{1+4 r^2} r d r$
$\text{B.}$ $\int_0^2 d \theta \int_1^2\left(2-r^2\right) \sqrt{1+4 r^2} r d r$
$\text{C.}$ $\int_0^{2 \pi} d \theta \int_{-1}^{\sqrt{2}}\left(2-r^2\right) r d r$
$\text{D.}$ $\int_0^{2 \pi} d \theta \int_0^{\sqrt{2}}\left(2-r^2\right) \sqrt{1+4 r^2} r d r$
如图, 正方形 $\{(x, y)|| x|\leq 1| y \mid, \leq 1\}$ 被其对角线划分为四个 区域 $D_k(k=1,2,3,4), I_k=\iint_{D_k} y \cos x \mathrm{~d} x \mathrm{~d} y$, 则 $\max _{1 \leq k \leq 4}\left\{I_k\right\}=$
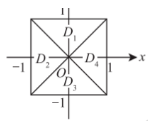
$\text{A.}$ $I_1$.
$\text{B.}$ $I_2$.
$\text{C.}$ $I_3$.
$\text{D.}$ $I_4$.
设区域 $D$ 由曲线 $y=\sin x, x= \pm \frac{\pi}{2}, y=1$ 围成, 则 $\iint_D\left(x y^5-1\right) \mathrm{d} x \mathrm{~d} y=$
$\text{A.}$ $\pi$.
$\text{B.}$ $2$.
$\text{C.}$ $-2$.
$\text{D.}$ $-\pi$.