一、单选题 （共 34 题，每小题 5 分，共 50 分，每题只有一个选项正确）
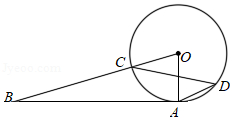
如图, $A B$ 为 $\odot O$ 的切线, 点 $A$ 为切点, $O B$ 交 $\odot O$ 于点 $C$, 点 $D$ 在 $\odot O$ 上, 连接 $A D 、 C D, O A$, 若 $\angle A D C=35^{\circ}$, 则 $\angle A B O$ 的度数为 （ ）
$\text{A.}$ $25^{\circ}$
$\text{B.}$ $20^{\circ}$
$\text{C.}$ $30^{\circ}$
$\text{D.}$ $35^{\circ}$
方程 $\frac{2}{x+5}=\frac{1}{x-2}$ 的解为 （ ）
$\text{A.}$ $x=-1$
$\text{B.}$ $x=5$
$\text{C.}$ $x=7$
$\text{D.}$ $x=9$
对于任意的有理数 $a, b$, 如果满足 $\frac{a}{2}+\frac{b}{3}=\frac{a+b}{2+3}$, 那么我们称这一对数 $a, b$ 为 “相随数 对”” 记为 $(a, b)$. 若 $(m, n)$ 是 “相随数对”, 则 $3 m+2[3 m+(2 n-1)]=(\quad)$
$\text{A.}$ -2
$\text{B.}$ -1
$\text{C.}$ 2
$\text{D.}$ 3
在式子 $\frac{x}{2}, \frac{x+y}{x-2 y}, \frac{x}{\pi}, \frac{2 x-y}{4}, \frac{1}{a}, 2 a$ 中,分式的个数在
$\text{A.}$ 1个
$\text{B.}$ 2个
$\text{C.}$ 3个
$\text{D.}$ 4个
把分式 $\frac{3 x-3 y}{x y}$ 中的 $x y$ 的值同时扩大为原来的 2 倍,则分式的值
$\text{A.}$ 不变
$\text{B.}$ 扩大为原来的 2 倍
$\text{C.}$ 扩大为原来的 4倍
$\text{D.}$ 缩小为原来的一半
化简 $\left(1-\frac{2 x-1}{x^2}\right) \div\left(1-\frac{1}{x^2}\right)$ 的结果为
$\text{A.}$ $\frac{x-1}{x+1}$
$\text{B.}$ $\frac{x+1}{x-1}$
$\text{C.}$ $\frac{x+1}{x}$
$\text{D.}$ $\frac{x-1}{x}$
化简 $\frac{2 a}{a^2-1}+\frac{1}{1-a}$ 的结果正确的是
$\text{A.}$ $\frac{3 a+1}{a^2-1}$
$\text{B.}$ $\frac{3 a-1}{a^2-1}$
$\text{C.}$ $\frac{1}{a+1}$
$\text{D.}$ $\frac{1}{a-1}$
化简 $\frac{x^2}{x-1}+\frac{1}{1-x}$ 的结果是
$\text{A.}$ $x+1$
$\text{B.}$ $\frac{1}{x+1}$
$\text{C.}$ $x-1$
$\text{D.}$ $\frac{x}{x-1}$
使分式 $\frac{x}{2 x-4}$ 有意义的 $x$ 的取值范围是
$\text{A.}$ $x=2$
$\text{B.}$ $x \neq 2$
$\text{C.}$ $x=-2$
$\text{D.}$ $x \neq 0$
与 $-3 \dfrac{1}{2}$ 相等的是
$\text{A.}$ $-3-\frac{1}{2}$
$\text{B.}$ $3-\frac{1}{2}$
$\text{C.}$ $-3+\frac{1}{2}$
$\text{D.}$ $3+\frac{1}{2}$
化简 $\frac{1}{a-3}-\frac{6}{a^2-9}$ 的结果是
$\text{A.}$ $\frac{1}{a+3}$
$\text{B.}$ $a-3$
$\text{C.}$ $a+3$
$\text{D.}$ $\frac{1}{a-3}$
若 $\frac{a}{b}=\frac{2}{3}$, 则 $\frac{a+b}{b}$ 等于
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{3}{5}$
$\text{D.}$ $\frac{5}{3}$
已知 $P=\frac{99^9}{9^{99}}, Q=\frac{11^9}{9^{90}}$, 那么 $P 、 Q$ 的大小关系是
$\text{A.}$ $P>Q$
$\text{B.}$ $P=Q$
$\text{C.}$ $P < Q$
$\text{D.}$ 无法确定
$a=\dfrac{19951995}{19961996}, b=\dfrac{19961996}{19971997}, c=\dfrac{19971997}{19981998}$, 则
$\text{A.}$ $a < b < c$
$\text{B.}$ $b < c < a$
$\text{C.}$ $c < b < a$
$\text{D.}$ $a < c < b$
如果关于 $x$ 的不等式组 $ \left\{\begin{array}{l}
\frac{x-m}{2} \geq 0 \\
x+3 < 3(x-1)
\end{array}\right.$ 的解集为 $x>3$, 且关于 $y$ 的分式方程 $\frac{3-y}{2-y}+\frac{m}{y-2}=3$ 有非负整数解, 则符合条件的整数 $m$ 的值的和是
$\text{A.}$ -4
$\text{B.}$ -3
$\text{C.}$ -1
$\text{D.}$ -7
若代数式 $\frac{2}{x-3}$ 有意义, 则实数 $x$ 的取值范围是
$\text{A.}$ $x=0$
$\text{B.}$ $x=3$
$\text{C.}$ $x \neq 0$
$\text{D.}$ $x \neq 3$
计算: $\frac{a^2-5 a}{a-5}=$
$\text{A.}$ $a-5$
$\text{B.}$ $a+5$
$\text{C.}$ 5
$\text{D.}$ $a$
若关于 $x$ 的不等式组 $\left\{\begin{array}{l}2\left(x+\frac{5}{2}\right)>11 \\ 3 x-a < 1\end{array}\right.$ 无解, 且关于 $y$ 的分式方程 $\frac{3 y}{y-2}+\frac{a+4}{2-y}=1$ 有非负整数解,则满足条件的所有整数 $a$ 的和为
$\text{A.}$ 8
$\text{B.}$ 10
$\text{C.}$ 16
$\text{D.}$ 18
若分式 $\frac{1}{x+1}$ 有意义, 则 $\mathrm{x}$ 的取值范围是
$\text{A.}$ $x \neq-1$
$\text{B.}$ $x \neq 0$
$\text{C.}$ $x \neq 1$
$\text{D.}$ $x \neq 2$
已知 $a 、 b 、 c$ 满足 $a+c=b$ ，且 $\frac{1}{a}+\frac{1}{b}=\frac{1}{c}$ ，则下列结论错误的是
$\text{A.}$ 若 $b>c>0$ ，则 $a>0$
$\text{B.}$ 若 $c=1$ ，则 $a(a-1)=1$
$\text{C.}$ 若 $b c=1$ ，则 $a=1$
$\text{D.}$ 若 $a^2-c^2=2$ 则$a c=2$
设 $M=\frac{1}{2018}+\frac{1}{2019}+\frac{1}{2020}+\cdots+\frac{1}{2050}$, 则 $\frac{1}{M}$ 的整数部分是
$\text{A.}$ 60
$\text{B.}$ 61
$\text{C.}$ 62
$\text{D.}$ 63
函数 $y=\frac{2 x}{1-x}$ 的自变量 $x$ 的取值范围是
$\text{A.}$ $x \neq 1$
$\text{B.}$ $x < 1$
$\text{C.}$ $x \neq 0$
$\text{D.}$ $x \leq 1$
要使分式 $\frac{2-x}{x-1}$ 有意义， $x$ 的取值范围满足
$\text{A.}$ $x \neq 1$
$\text{B.}$ $x \neq 0$
$\text{C.}$ $x \neq 2$
$\text{D.}$ $x \neq-1$
如图, 将图 1 中的菱形纸片沿对角线剪成 4 个直角三角形, 拼成如图 2 的四边形 $A B C D$ (相邻纸片之间不重叠, 无缝隙). 若四边形 $A B C D$ 的面积为 13, 中间空白处的四边形 $E F G H$的面积为 1 , 直角三角形的两条直角边分别为 $a$ 和 $b$, 则 $(a+b)^2=$
$\text{A.}$ 12
$\text{B.}$ 13
$\text{C.}$ 24
$\text{D.}$ 25
如图, $\angle A B C=90^{\circ}, A B=6, B C=8, A D=C D=7$, 若点 $P$ 到 $A C$ 的距离为
5, 则点 $P$ 在四边形 $A B C D$ 边上的个数为
$\text{A.}$ 0个
$\text{B.}$ 2个
$\text{C.}$ 3个
$\text{D.}$ 4个
如图, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}$, 以其三边为边在 $\mathrm{AB}$ 的同侧作三个正方形, 点 $\mathrm{F}$ 在 $\mathrm{GH}$ 上, $\mathrm{CG}$ 与 $\mathrm{EF}$ 交于点 $\mathrm{P}, \mathrm{CM}$ 与 $\mathrm{BE}$ 交于点 $Q$. 若 $H F=F G$, 则西四边形 $P C Q E$ 的值是
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{5}$
$\text{C.}$ $\frac{\sqrt{3}}{12}$
$\text{D.}$ $\frac{6}{25}$
化简 $\frac{x}{x-1}+\frac{1}{1-x}$ 的结果是
$\text{A.}$ $\frac{x+1}{x-1}$
$\text{B.}$ 1
$\text{C.}$ $\frac{x-1}{x+1}$
$\text{D.}$ -1
如图，在 $\square A B C D$ 中， $\angle B=60^{\circ} ， A B=6 \mathrm{~cm} ， B C=12 \mathrm{~cm}$. A点 $\mathrm{P}$ 从点A出发、以 $1 \mathrm{~cm} / s$ 的速度沿 $A \rightarrow D$ 运动，同时点 $\mathrm{Q}$ 从点C出发，以 以 $\mathrm{cm} / s$ 的速度沿 $C \rightarrow B \rightarrow C \rightarrow \cdots$ 往复运动，当点 $\mathrm{P}$ 到达端点 $\mathrm{D}$ 时，点 $\mathrm{Q}$ 随之停止运动. 在此运动过程中，线段 $P Q=C D$ 出现的次数是
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 6
如图，在矩形 $A B C D$ 中， $A F$ 平分 $\angle B A C$ ，将矩形沿直线 $E F$ 折叠，使点$A，B$分别落在边 $A D 、 B C$ 上的点 $A^{\prime} ， B^{\prime}$ 处，$EF$， $A^{\prime} F$ 分别交 $A C$ 于点$G，H$.若 $G H=2, H C=8$ ，则 $B F$ 的长为
$\text{A.}$ $\frac{20 \sqrt{2}}{9}$
$\text{B.}$ $\frac{20 \sqrt{3}}{9}$
$\text{C.}$ $\frac{5 \sqrt{3}}{2}$
$\text{D.}$ 5
如图，在正方形 $A B C D$ 的边 $C D$ 上有一点 $E$ ，连接 $A E$ ，把 $A E$ 绕点 $E$ 逆时针旋转 $90^{\circ}$ ，得到 $F E$ ，连接 $C F$ 并延长与 $A B$ 的延长线交于点 $G$. 则 $\frac{F G}{C E}$ 的值为
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ $\frac{3 \sqrt{2}}{2}$
$\text{D.}$ $\frac{3 \sqrt{3}}{2}$
四边形 $A B C D$ 为矩形, 过 $A 、 C$ 作对角线 $B D$ 的垂线, 过 $B 、 D$ 作对角线 $A C$ 的垂线. 如果四个垂线拼成一个四边形,那这个四边形为
$\text{A.}$ 菱形
$\text{B.}$ 矩形
$\text{C.}$ 直角梯形
$\text{D.}$ 等腰梯形
如图, 矩形 $A B C D$ 中, $A B=\sqrt{3}, B C=1$, 动点 $E, F$ 分别从点 $A, C$ 同时出发, 以每秒 1 个单位长度的速度沿 $A B, C D$ 向终点 $B, D$ 运动, 过点 $E, F$ 作直线 $l$, 过点 $A$ 作直线 $l$ 的垂线, 垂足为 $G$, 则 $A G$ 的最大值为
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ 2
$\text{D.}$ 1
图 1 是第七届国际数学教育大会 (ICME) 的会徽, 图 2 由其主体图案中相邻两个直角三角形组合而成. 作菱形 $C D E F$, 使点 $D, E, F$ 分别在边 $O C, O B$, $B C$ 上, 过点 $E$ 作 $E H \perp A B$ 于点 $H$. 当 $A B=B C, \angle B O C=30^{\circ}, D E=2$ 时, $E H$ 的长为
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ $\sqrt{2}$
$\text{D.}$ $\frac{4}{3}$
如图, 四边形 $A B C D$ 内接于e $O, B C / / A D, A C \perp B D$. 若 $\angle A O D=120^{\circ}$, $A D=\sqrt{3}$, 则 $\angle C A O$ 的度数与 $B C$ 的长分别为
$\text{A.}$ $10^{\circ}, 1$
$\text{B.}$ $10^{\circ}, \sqrt{2}$
$\text{C.}$ $15^{\circ}, 1$
$\text{D.}$ $15^{\circ}, \sqrt{2}$
二、填空题 （共 47 题, 每小题 5 分，共 20 分， 请把答案直接填写在答题纸上）
若扇形的圆心角为$30^0$ ，半径为17，则扇形的弧长为
如图，圆$O$与$\triangle ABC$ 的边$B$相切，切点为B, $\triangle ABC$将 绕点B 按顺时针方向旋转得到$\triangle O'A'B$ ，使点$O'$ 落在圆O上，边A'B 交线段AO于点C 若 $\angle a'=25^0$，则 $\angle OCB$= （ ） 度．
在函数 $y=\frac{x}{x-7}$ 中, 自变量 $x$ 的取值范围是 （ ）
一个扇形的面积是 $13 \pi \mathrm{cm}^{2}$, 半径是 $6 \mathrm{~cm}$, 则此扇形的圆心角是
（ ） 度.
先化简, 再求代数式 $\left(1-\frac{2}{x+1}\right) \div \frac{x^{2}-1}{2 x+2}$ 的值, 其中 $x=4 \cos 30^{\circ}-1$.
要使分式 $\frac{x+2}{x-1}$ 有意义, $x$ 需满足的条件是