单选题 (共 6 题 ),每题只有一个选项正确
在 Rt $\triangle A B C$ 中, $\angle C=90^{\circ}, \sin A=\frac{3}{5}$, 则 $\cos A$ 的值是
$\text{A.}$ $\frac{3}{5}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $\frac{4}{5}$
$\text{D.}$ $\frac{5 \sqrt{34}}{34}$
已知 “ $\alpha$ 为锐角时, $\sin \alpha$ 随着 $\alpha$ 的增大而增大”, 则 $\sin 37^{\circ}$ 的值更靠近
$\text{A.}$ $\frac{2}{5}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{4}{5}$
$\text{D.}$ $\frac{5}{6}$
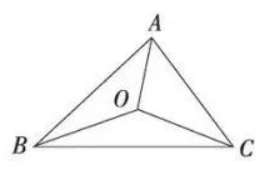
如图, 在 $\triangle A B C$ 中, $A B=8, A C=6, O$ 为 $\triangle A B C$ 的内心, 若 $\triangle A B O$ 的面积为 20 , 则 $\triangle A C O$ 的 面积为
$\text{A.}$ 20
$\text{B.}$ 15
$\text{C.}$ 18
$\text{D.}$ 12
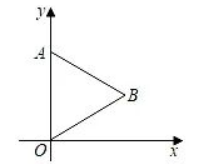
如图, 将等边 $\triangle A O B$ 放在平面直角坐标系中, 点 $A$ 的坐标为 $(0,4)$, 点 $B$ 在第一象限, 将等边 $\triangle A O B$ 绕 点 $O$ 顺时针旋堑 $180^{\circ}$ 得到 $\triangle A^{\prime} O B^{\prime}$ ,则点 $B$ 的对应点 $B^{\prime}$ 的坐标是
$\text{A.}$ $(2 \sqrt{3}, 2)$
$\text{B.}$ $(2 \sqrt{3},-2)$
$\text{C.}$ $(-2 \sqrt{3},-2)$
$\text{D.}$ $(0,-4)$
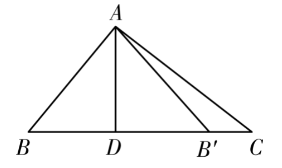
如图,在Rt $\triangle A B C$ 中, $\angle B A C=90^{\circ} , \angle B=50^{\circ} , A D \perp B C$ ,垂足为 $D , \triangle A D B$ 与 $\triangle A D B^{\prime}$ 关于直线 $A D$ 对称,点 $B$ 的对称点是点 $B^{\prime}$ ,则 $\angle C A B^{\prime}$ 的度数为
$\text{A.}$ $10^{\circ}$
$\text{B.}$ $20^{\circ}$
$\text{C.}$ $30^{\circ}$
$\text{D.}$ $40^{\circ}$
如图,在 $\triangle A B C$ 中, $D 、 E$ 分别为线段 $B C 、 B A$ 的中点,设 $\triangle A B C$ 的面积为 $S_1, \triangle E B D$ 的面 积为 $S_2$ ,则 $\frac{S_2}{S_1}=$
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{7}{8}$