如图, 直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 中, 底面 $A B C D$ 是菱形, 其所在平面为 $\alpha$, 且 $\angle B A D=60^{\circ}$, $A B=2 A A_1=2 . O$ 是 $A C, B D$ 的交点, $P$ 是平面 $\alpha$ 内的动点(图中未画出). 则下列说法正确的是
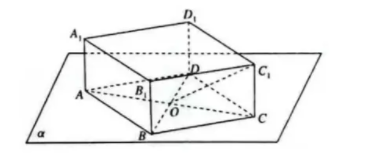
A
若 $C_1 P=2$, 则动点 $P$ 的轨迹长度为 $2 \pi$
B
若 $\angle O C_1 P=90^{\circ}$, 则动点 $P$ 的轨迹是一条直线
C
若 $O P=C_1 P$, 则动点 $P$ 的轨迹是一条直线
D
若动点 $P$ 到直线 $O C_1$ 的距离为 1 , 则 $P A+P C$ 为定值
E
F