单选题 (共 11 题 ),每题只有一个选项正确
已知集合 $A=\left\{x \mid 2^x < 4\right\}, B=\left\{x \left\lvert\, \log _{\frac{1}{3}} x>-1\right.\right\}$, 则 $A \cap B=(\quad$
$\text{A.}$ $(0,2)$
$\text{B.}$ $(-\infty, 2)$
$\text{C.}$ $(-\infty, 3)$
$\text{D.}$ $\varnothing$
已知 $(2 x+1)^5=a_0+a_1 x+a_2 x^2+\cdots+a_5 x^5$, 则 $a_2=(\quad)$
$\text{A.}$ 10
$\text{B.}$ 20
$\text{C.}$ 40
$\text{D.}$ 80
已知 $\left\{a_n\right\}$ 是无穷数列, $a_1=3$, 则 "对任意的 $m, n \in \mathbf{N}^*$, 都有 $a_{m+n}=a_m+a_n$ " 是 " $\left\{a_n\right\}$ 是等差数列"的 ( )
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
损尖式屋顶是中国古代传统建筑的一种屋顶样式, 如图所示的建筑屋顶是圆形损尖, 可近似看作一个圆锥, 已知该圆锥的底面直径为 8 m , 高为 3 m , 则该屋顶的面积约为

$\text{A.}$ $15 \pi \mathrm{m}^2$
$\text{B.}$ $20 \pi \mathrm{m}^2$
$\text{C.}$ $24 \pi \mathrm{m}^2$
$\text{D.}$ $30 \pi \mathrm{m}^2$
已知抛物线 $C: y^2=2 p x(p>0)$ 的焦点为 $F$, 若抛物线上一点 $M$ 满足 $|M F|=2, \angle O F M=60^{\circ}$, 则 $p=(\quad)$
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 6
$\text{D.}$ 8
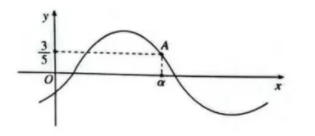
如图, $A\left(\alpha, \frac{3}{5}\right)$ 是函数 $y=\sin \left(x-\frac{\pi}{6}\right)$ 图象上的一点, 则 $\tan \left(2 \alpha+\frac{\pi}{6}\right)=(\quad)$
$\text{A.}$ $-\frac{24}{7}$
$\text{B.}$ $\frac{24}{7}$
$\text{C.}$ $-\frac{7}{24}$
$\text{D.}$ $\frac{7}{24}$
已知函数 $f(x)$, 对任意的 $x, y \in \mathbf{R}$ 都有 $f(x+y)=2^x f(y)+2^y f(x)$, 且 $f(1)=2$, 则下列说法不正确的是
$\text{A.}$ $f(0)=0$
$\text{B.}$ $\frac{f(x)}{2^x}$ 是奇函数
$\text{C.}$ $y=f(x)$ 是 $\mathbf{R}$ 上的增函数
$\text{D.}$ $f(n)=n \cdot 2^n\left(n \in \mathbf{N}^*\right)$
已知直线 $l_1: a x-y+5=0$ 与直线 $l_2: x+a y-a+4=0(a \in \mathbf{R})$ 的交点为 $P$, 则点 $P$ 到直线 $l: y=x-3$ 距离的取值范围是()
$\text{A.}$ $[3 \sqrt{2}, 7 \sqrt{2}]$
$\text{B.}$ $(3 \sqrt{2}, 7 \sqrt{2}]$
$\text{C.}$ $[2 \sqrt{2}, 6 \sqrt{2}]$
$\text{D.}$ $(2 \sqrt{2}, 6 \sqrt{2}]$
已知向量 $\vec{a}=(1,2), \vec{b}=(2,-1)$, 则下列判断正确的是 ( )
$\text{A.}$ $\vec{a}+\vec{b}=(3,1)$
$\text{B.}$ $\vec{a} \cdot \vec{b}=(2,-2)$
$\text{C.}$ $\vec{a} \perp \vec{b}$
$\text{D.}$ $|\vec{a}|=|\vec{b}|$
现统计具有线性相关关系的变量 $X, Y, Z$ 的 $n$ 组数据, 如下表所示:

并对它们进行相关性分析, 得到 $Z=b_1 X+a_1, Z$ 与 $X$ 的相关系数是 $r_1, Z=b_2 Y+a_2, Z$ 与 $Y$ 的相关系数是 $r_2$, 则下列判断正确的是 $(\quad)$
附: 经验回归方程 $\hat{y}=\hat{b} x+\hat{a}$ 中斜率和截距的最小二乘估计公式分别为 $\hat{b}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}$, $\hat{a}=\bar{y}-\hat{b} \bar{x}$, 相关系数 $r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \sqrt{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}$.
$\text{A.}$ $\bar{y}=10 \bar{x}$
$\text{B.}$ $\sigma_2^2=10 \sigma_1^2$
$\text{C.}$ $b_1=10 b_2$
$\text{D.}$ $r_2=r_1$
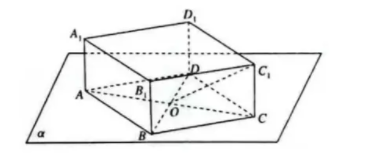
如图, 直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 中, 底面 $A B C D$ 是菱形, 其所在平面为 $\alpha$, 且 $\angle B A D=60^{\circ}$, $A B=2 A A_1=2 . O$ 是 $A C, B D$ 的交点, $P$ 是平面 $\alpha$ 内的动点(图中未画出). 则下列说法正确的是
$\text{A.}$ 若 $C_1 P=2$, 则动点 $P$ 的轨迹长度为 $2 \pi$
$\text{B.}$ 若 $\angle O C_1 P=90^{\circ}$, 则动点 $P$ 的轨迹是一条直线
$\text{C.}$ 若 $O P=C_1 P$, 则动点 $P$ 的轨迹是一条直线
$\text{D.}$ 若动点 $P$ 到直线 $O C_1$ 的距离为 1 , 则 $P A+P C$ 为定值
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知复数 $z$ 的实部为 2 , 且 $\frac{z}{2+i}$ 为纯虚数, 则复数 $z=$
已知双曲线 $C: x^2-y^2=9$, 点 $N$ 的坐标为 $(m, n)$, 其中 $m, n \in\{1,2,3\}$, 存在过点 $N$ 的直线与双曲线 $C$ 相交于 $A, B$ 两点, 且点 $N$ 为弦 $A B$ 的中点, 则点 $N$ 的坐标是 $\qquad$ . (写出一个符合条件的答案即可)
已知 $a>0$ 且 $x>0$ 时, 不等式 $a \mathrm{e}^{2 x}-\ln (x+m)+\frac{1}{4 a}>0$ 恒成立, 则正数 $m$ 的取值范围是
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=2 x^3-3 a x^2+1$.
(1) 当 $a=1$ 时, 求函数 $f(x)$ 的单调递减区间;
(2) 若 $x=0$ 是函数 $f(x)$ 的极小值点, 求实数 $a$ 的取值范围.
某市为了解车主用车的能源类型与对该市交通拥堵感受的关系, 共调查了 100 名车主, 并得到如下的 $2 \times 2$ 列联表:

(1) 将频率估计为概率, 从该市燃油车和新能源车车主中随机抽取 1 名, 记 "抽取到燃油车车主" 为事件 $A_1$, "抽取到新能源车车主" 为事件 $A_2$, "抽取到的车主觉得交通拥堵" 为事件 $B_1$, "抽取到的车主觉得交通不拥堵" 为事件 $B_2$, 计算 $P\left(B_1 \mid A_1\right), P\left(B_1 \mid A_2\right)$, 比较它们的大小, 并说明其意义;
(2) 是否有 $90 \%$ 的把握认为该市车主用车的能源类型与对该市交通拥堵的感受有关? 将分析结果与 (1)中结论进行比较, 并作出解释.
附表及公式:

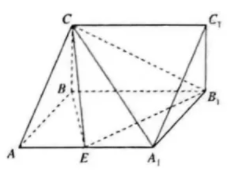
如图, 已知斜三棱柱 $A B C-A_1 B_1 C_1$ 中, 侧面 $B B_1 C_1 C \perp$ 侧面 $A A_1 B_1 B$, 侧面 $B B_1 C_1 C$ 是矩形,侧面 $A A_1 B_1 B$ 是菱形, $\angle B A A_1=60^{\circ}, A B=2 B C=2$, 点 $E$ 是棱 $A A_1$ 的中点.
(1) 证明: $B E \perp$ 平面 $B B_1 C_1 C$;
(2) 求二面角 $A_1-B_1 C-E$ 的余弦值.
已知直线 $l: x=2$ 经过椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的右焦点 $F$ 且被椭圆 $C$ 截得的弦长为 $2 \sqrt{2}$.
(1) 求椭圆 $C$ 的方程:
(2) 若过点 $P(4,0)$ 的动直线 $m$ 与椭圆 $C$ 相交于 $A, B$ 两点, 且直线 $l$ 上的点 $M$ 满足 $\overrightarrow{A M} / / \overrightarrow{F P}$, 求证:直线 $M B$ 过定点, 并求该定点的坐标.
二进制是在数学和数字电路中以 2 为基数的记数系统, 在这一系统中, 通常用两个不同的符号 0,1 来表示数. 如果十进制中的整数 $n=a_k \cdot 2^k+a_{k-1} \cdot 2^{k-1}+\cdots+a_1 \cdot 2+a_0\left(a_i \in\{0,1\}, i=0,1, \cdots, k\right)$,则这个数在二进制下记为 $a_k a_{k-1} \cdots a_1 a_0$, 即 $(n)_{10}=\left(a_k a_{k-1} \cdots a_1 a_0\right)_2$. 记十进制下的整数 $n$ 在二进制表示下的各位数字之和为 $\varphi(n)$, 即 $\varphi(n)=a_0+a_1+\cdots+a_k$.
(1) 计算 $\varphi(7)$;
(2) 证明: $\varphi(4 n+3)=\varphi(2 n+1)+1$ ;
(3) 求数列 $\left\{\varphi\left(3 \cdot 2^n-1\right)\right\}$ 的前 $n$ 项和 $S_n$.