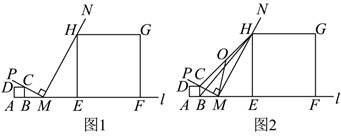
如图, 点 $A 、 B 、 M 、 E 、 F$ 依次在直线 $l$ 上, 点 $A 、 B$ 固定不动, 且 $A B=2$, 分别以 $A B 、 E F$ 为边在直线 $l$ 同侧作正方形 $A B C D$ 、正方形 $E F G H, \angle P M N=90^{\circ}$, 直角边 $M P$ 恒过点 $C$, 直角边 $M N$ 恒过点 $H$.
(1) 如图1, 若 $B E=10, E F=12$, 求点 $M$ 与点 $B$ 之间的距离;
(2) 如图1, 若 $B E=10$, 当点 $M$ 在点 $B 、 E$ 之间运动时, 求 $H E$ 的最大值;
(3) 如图2, 若 $B F=22$, 当点 $E$ 在点 $B 、 F$ 之间运动时, 点 $M$ 随之运动, 连接 $C H$, 点 $O$ 是 $C H$ 的中点, 连接 $H B 、 M O$, 则 $2 O M+H B$ 的最小值为